【题目】已知函数![]() .
.
(1)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为正整数,方程
为正整数,方程![]() 的两个实数根
的两个实数根![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)11.
;(2)11.
【解析】试题分析:(1)存在![]() ,使得
,使得![]() 等价于
等价于![]() 在
在![]() 上有两个不等实根,或
上有两个不等实根,或![]() 在
在![]() 上有两个不等实根,结合二次函数的顶点在直线下方或上方列不等式组求解即可;(2)利用一元二次方程方程根的分别,列不等式组,根据
上有两个不等实根,结合二次函数的顶点在直线下方或上方列不等式组求解即可;(2)利用一元二次方程方程根的分别,列不等式组,根据![]() 为正整数,先初步判断
为正整数,先初步判断![]() 的范围,再利用分类讨论思想求解即可.
的范围,再利用分类讨论思想求解即可.
试题解析:(1)当![]() 时,
时, ![]()
由题意可知, ![]() 在
在![]() 上有两个不等实根,或
上有两个不等实根,或![]() 在
在![]() 上有两个不等实根,则
上有两个不等实根,则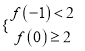 或
或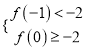 ,
,
解得![]() 或
或![]()
即实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(2)设![]() ,则由题意得
,则由题意得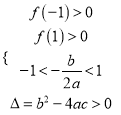 ,即
,即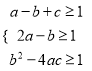 ,
,
所以![]() ,由于
,由于![]()
①当![]() 时,
时, ![]() ,且
,且![]() 无解,
无解,
②当![]() 时,
时, ![]() ,且
,且![]() ,于是
,于是![]() 无解,
无解,
③当![]() 时,
时, ![]() ,且
,且![]() ,由
,由![]() ,得
,得![]() ,此时有解
,此时有解![]() ,
,
综上所述, ![]() ,当
,当![]() 时取等号,即
时取等号,即![]() 的最小值为11.
的最小值为11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为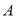 ,离心离为
,离心离为 ,点
,点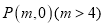 满足条件
满足条件 .
.(Ⅰ)求
 的值.
的值.(Ⅱ)设过点
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,记
两点,记 和
和 的面积分别为
的面积分别为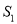 、
、 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是直角梯形,
是直角梯形,  ,又
,又 ,直线
,直线 与直线
与直线 所成的角为
所成的角为 .
.
(1)求证:
 ;
;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知中心在原点,焦点在
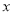 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为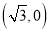 ,
, 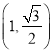 是椭圆上的一个点.
是椭圆上的一个点.(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为
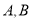 ,
, 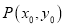 (
(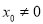 )是椭圆上异于
)是椭圆上异于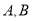 的任意一点,
的任意一点, 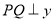 轴,
轴, 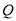 为垂足,
为垂足, 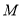 为线段
为线段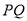 中点,直线
中点,直线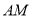 交直线
交直线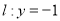 于点
于点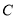 ,
, 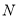 为线段
为线段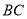 的中点,如果
的中点,如果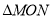 的面积为
的面积为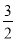 ,求
,求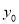 的值.
的值.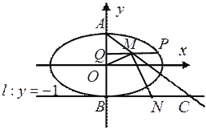
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入
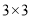 的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )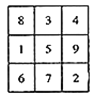
A. 9 B. 8 C. 6 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中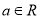 ,
, 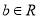 .
.(Ⅰ)当
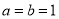 时,
时, 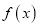 的零点为______;(将结果直接填写在横线上)
的零点为______;(将结果直接填写在横线上)(Ⅱ)当
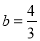 时,如果存在
时,如果存在 ,使得
,使得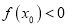 ,试求
,试求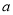 的取值范围;
的取值范围;(Ⅲ)如果对于任意
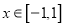 ,都有
,都有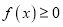 成立,试求
成立,试求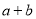 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018吉林长春高三下学期二模】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如下图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
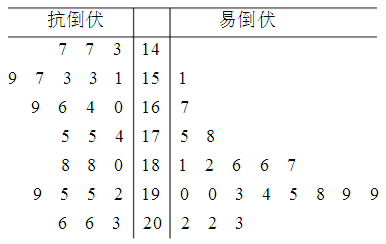
(I)完成列
 联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?(II)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?

相关试题

