【题目】过椭圆 ![]() =1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且
=1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且 ![]() 共线.
共线.
(1)求椭圆的离心率;
(2)当三角形AOB的面积S△AOB= ![]() 时,求椭圆的方程.
时,求椭圆的方程.
参考答案:
【答案】
(1)解:设AB:y=﹣x+c,直线AB交椭圆于两点,A(x1,y1),B(x2,y2),
![]() ,b2x2+a2(﹣x+c)2=a2b2,
,b2x2+a2(﹣x+c)2=a2b2,
(b2+a2)x2﹣2a2cx+a2c2﹣a2b2=0,
![]() ,
, ![]() ,
, ![]() =(x1+x2,y1+y2),与
=(x1+x2,y1+y2),与 ![]() =
= ![]() 共线,
共线,
可得3(y1+y2)﹣(x1+x2)=0,3(﹣x1+c﹣x2+c)﹣(x1+x2)=0 ![]()
(2)解:由a2=3b2,可设椭圆的方程为: ![]() ,c2=3b2﹣b2=2b2,
,c2=3b2﹣b2=2b2, ![]() ,
,
AB:y=﹣x+ ![]() b,
b,  ,可得:
,可得: ![]() ,
,
即 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
AB的距离为:|AB|= ![]() =
= ![]() =
= ![]() ,
,
O到AB距离 ![]() .
.
![]() ,
,
椭圆方程为 ![]() .
.
【解析】(1)设直线AB的方程,A,B的坐标,联立直线的方程和椭圆的方程,利用韦达定理,通过![]() +
+![]() 与
与![]() 共线,可求出椭圆的离心率;(2)设椭圆的方程和直线的方程,联立方程组,通过韦达定理求出|AB|,O到直线AB的距离 ,利用三角形的面积,可求出椭圆的方程.
共线,可求出椭圆的离心率;(2)设椭圆的方程和直线的方程,联立方程组,通过韦达定理求出|AB|,O到直线AB的距离 ,利用三角形的面积,可求出椭圆的方程.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若
 =0,
=0, 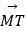 =
=  ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中,  ,
,  为线段
为线段 (含端点)上一个动点,设
(含端点)上一个动点,设 对于函数
对于函数 ,给出以下三个结论:
,给出以下三个结论:①当
 时,函数
时,函数 的值域为
的值域为 ;
;②对于任意的
 ,均有
,均有 ;
;③对于任意的
 ,函数
,函数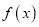 的最大值均为4.
的最大值均为4.其中所有正确的结论序号为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣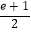 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ <a<﹣
<a<﹣  时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据平面向量基本定理,若
 为一组基底,同一平面的向量
为一组基底,同一平面的向量 可以被唯一确定地表示为
可以被唯一确定地表示为  =
=  ,则向量
,则向量 与有序实数对
与有序实数对 一一对应,称
一一对应,称 为向量
为向量 的基底
的基底 下的坐标;特别地,若
下的坐标;特别地,若 分别为
分别为 轴正方向的单位向量
轴正方向的单位向量 ,则称
,则称 为向量
为向量 的直角坐标.
的直角坐标.(I)据此证明向量加法的直角坐标公式:若
 ,则
,则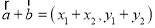 ;
;(II)如图,直角
 中,
中,  ,
,  点在
点在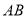 上,且
上,且 ,求向量
,求向量 在基底
在基底 下的坐标.
下的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
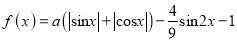 ,若
,若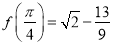
(1)求
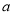 的值,并写出函数
的值,并写出函数 的最小正周期(不需证明);
的最小正周期(不需证明);(2)是否存在正整数
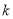 ,使得函数
,使得函数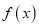 在区间
在区间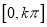 内恰有
内恰有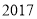 个零点?若存在,求出
个零点?若存在,求出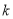 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

