【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() 为线段
为线段![]() (含端点)上一个动点,设
(含端点)上一个动点,设![]() 对于函数
对于函数![]() ,给出以下三个结论:
,给出以下三个结论:
①当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ;
;
②对于任意的![]() ,均有
,均有![]() ;
;
③对于任意的![]() ,函数
,函数![]() 的最大值均为4.
的最大值均为4.
其中所有正确的结论序号为__________.

参考答案:
【答案】②③
【解析】如图所示,建立直角坐标系.

∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),
∴B(0,0),A(﹣2,0),D(﹣1,a),C(0,a).
∵![]() =x
=x![]() ,(0≤x≤1).
,(0≤x≤1).
∴![]() =(﹣2,0)+x(1,a)=(x﹣2,xa),
=(﹣2,0)+x(1,a)=(x﹣2,xa),
∴![]() =
=![]() =(0,a)﹣(x﹣2,xa)=(2﹣x,a﹣xa)
=(0,a)﹣(x﹣2,xa)=(2﹣x,a﹣xa)
∴y=f(x)=![]() =(2﹣x,﹣xa)(2﹣x,a﹣xa)
=(2﹣x,﹣xa)(2﹣x,a﹣xa)
=(2﹣x)2﹣ax(a﹣xa)
=(a2+1)x2﹣(4+a2)x+4.
①当a=2时,y=f(x)=5x2﹣8x+4=![]() ,
,
∵0≤x≤1,∴当x=![]() 时,f(x)取得最小值
时,f(x)取得最小值![]() ;
;
又f(0)=4,f(1)=1,∴f(x)max=f(0)=4.
综上可得:函数f(x)的值域为![]() .
.
因此①不正确.
②由y=f(x)=(a2+1)x2﹣(4+a2)x+4.
可得:a∈(0,+∞),都有f(1)=1成立,因此②正确;
③由y=f(x)=(a2+1)x2﹣(4+a2)x+4.
可知:对称轴x0= .
.
当0<a≤![]() 时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.
时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.
当![]() 时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.
时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.
又f(0)=4,f(1)=1,∴f(x)max=f(0)=4.
因此③正确.
综上可知:只有②③正确.
故答案为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设z1 , z2是复数,给出下列四个命题:
①若|z1﹣z2|=0,则 =
=  ②若z1=
②若z1=  ,则
,则  =z2
=z2
③若|z1|=|z2|,则z1 =z2
=z2  ④若|z1|=|z2|,则z12=z22
④若|z1|=|z2|,则z12=z22
其中真命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2+bx,其中函数g(x)的图象在点(1,g(1))处的切线平行于x轴.
(1)确定a与b的关系;
(2)若a≥0,试讨论函数g(x)的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若
 =0,
=0, 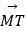 =
=  ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣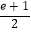 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ <a<﹣
<a<﹣  时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
 =1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且
=1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且  共线.
共线.
(1)求椭圆的离心率;
(2)当三角形AOB的面积S△AOB= 时,求椭圆的方程.
时,求椭圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值.
相关试题

