【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时
(万元);当年产量不小于80千件时![]() (万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
参考答案:
【答案】(1)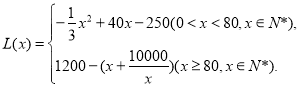 ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)当![]() ,
,![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 时,
时,![]()
![]() ;(2)分段函数两段分别用单调性和基本不等式求最小值,在比较两最小值的大小即可 .
;(2)分段函数两段分别用单调性和基本不等式求最小值,在比较两最小值的大小即可 .
试题解析:(1)当![]() ,
,![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 时,
时,
![]()
![]() ,
,
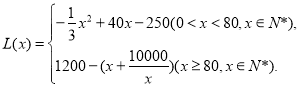
(2)当![]() ,
,![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
当![]() ,
,![]() 时,
时,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
综上所述,当![]() 时,
时,![]() 取得最大值1000,
取得最大值1000,
即年产量为100千件时,该厂在这一商品的生产中所获利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
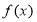 满足:对任意
满足:对任意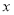 ,
,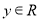 ,都有
,都有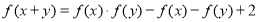 成立,且
成立,且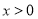 时,
时,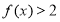 .
.(1)求
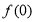 的值,并证明:当
的值,并证明:当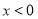 时,
时,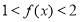 ;
;(2)判断
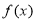 的单调性并加以证明;
的单调性并加以证明;(3)若函数
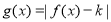 在
在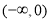 上递减,求实数
上递减,求实数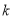 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
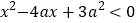 ,其中
,其中 ,命题
,命题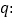 实数
实数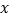 满足
满足|x-3|≤1 .
(1)若
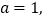 且
且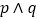 为真,求实数
为真,求实数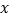 的取值范围;
的取值范围;(2)若
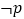 是
是
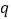 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
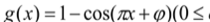 的图象过
的图象过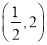 ,若有4个不同的正数
,若有4个不同的正数 满足
满足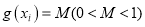 ,且
,且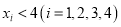 ,则从这四个数中任意选出两个,它们的和不超过5的概率为
,则从这四个数中任意选出两个,它们的和不超过5的概率为A.
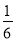 B.
B. 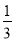 C.
C. 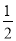 D.
D. 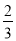
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
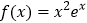 .
.(Ⅰ)求曲线
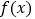 在点
在点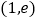 处的切线方程;
处的切线方程;(Ⅱ)若
 对
对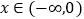 恒成立,求实数
恒成立,求实数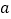 的取值范围;
的取值范围;(Ⅲ)求整数
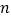 的值,使函数
的值,使函数 在区间
在区间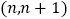 上有零点.
上有零点. -
科目: 来源: 题型:
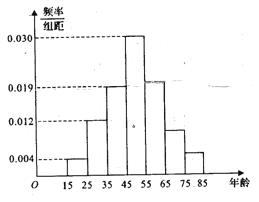
查看答案和解析>>【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在
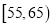 ,
, 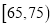 ,
, 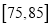 对应的小矩形的面积分别是
对应的小矩形的面积分别是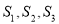 ,且
,且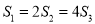 .
.
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在
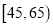 的人数;
的人数;(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在
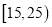 ,
, 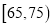 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在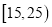 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
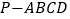 中,底面
中,底面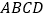 为平行四边形,
为平行四边形, 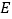 为侧棱
为侧棱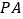 的中点.
的中点.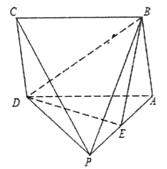
(Ⅰ)求证:
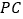 ∥平面
∥平面
(Ⅱ)若
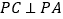 ,
,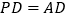 ,
,求证:平面

 平面
平面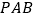
相关试题

