【题目】已知函数![]() 满足:对任意
满足:对任意![]() ,
,![]() ,都有
,都有![]() 成立,且
成立,且![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明:当
的值,并证明:当![]() 时,
时,![]() ;
;
(2)判断![]() 的单调性并加以证明;
的单调性并加以证明;
(3)若函数![]() 在
在![]() 上递减,求实数
上递减,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ,证明见解析;(2)
,证明见解析;(2)![]() 在
在![]() 上是增函数,证明见解析;(3)
上是增函数,证明见解析;(3)![]() .
.
【解析】
试题分析:(1)令![]() 可求得
可求得![]() 或
或![]() ,根据
,根据![]() 时,
时,![]() 可排除
可排除![]() ,设
,设![]() ,则
,则![]() ,那么
,那么![]() ,再由
,再由![]() 可得结论;(2)设
可得结论;(2)设![]() ,则
,则![]() ,∴
,∴![]() ,可证
,可证![]() ;(3)若函数
;(3)若函数![]() 在
在![]() 上递减,即
上递减,即![]() 时,
时,![]() ,根据单调性,
,根据单调性,![]()
![]() ,进而
,进而![]() .
.
试题解析:(1)∵![]() ,
,
∴![]() ,
,![]() 或
或![]() .
.
若![]() ,则
,则![]() ,
,
与已知条件![]() 时,
时,![]() 相矛盾,
相矛盾,
所以![]() .
.
设![]() ,则
,则![]() ,那么
,那么![]() .
.
又![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,从而
,从而![]() .
.
(2)函数![]() 在
在![]() 上是增函数,设
上是增函数,设![]() ,则
,则![]() ,∴
,∴![]() ,
,
![]()
![]() ,
,
∵由(1)可知对任意![]() ,
,![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]()
![]() ,
,
即![]() ,
,
∴函数![]() 在
在![]() 上是增函数.
上是增函数.
(3)∵由(2)知函数![]() 在
在![]() 上是增函数,
上是增函数,
∴函数![]() 在
在![]() 上也是增函数,若函数
上也是增函数,若函数![]() 在
在![]() 上递减,
上递减,
则当![]() 时,
时,![]() ,即
,即![]() 时,
时,![]() ,
,
∵![]() 时,
时,![]()
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的空间几何体中,平面
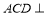 平面
平面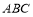 ,
,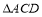 与
与 都是边长为2的等边三角形,
都是边长为2的等边三角形,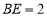 ,
,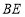 与平面
与平面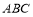 所成的角为
所成的角为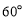 ,且点E在平面
,且点E在平面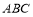 上的射影落在
上的射影落在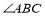 的平分线上.
的平分线上.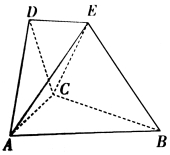
(1)求证:
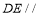 平面
平面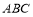 ;
;(2)求二面角
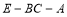 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别
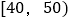
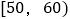
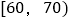
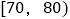
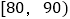
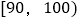
频数
6
18
28
26
17
5
(1)试估计该年级成绩
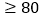 分的学生人数;
分的学生人数;(2)已知样本中成绩在
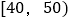 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
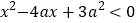 ,其中
,其中 ,命题
,命题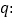 实数
实数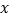 满足
满足|x-3|≤1 .
(1)若
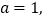 且
且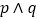 为真,求实数
为真,求实数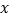 的取值范围;
的取值范围;(2)若
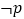 是
是
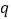 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
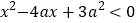 ,其中
,其中 ,命题
,命题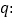 实数
实数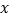 满足
满足|x-3|≤1 .
(1)若
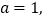 且
且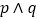 为真,求实数
为真,求实数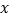 的取值范围;
的取值范围;(2)若
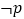 是
是
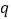 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
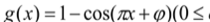 的图象过
的图象过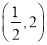 ,若有4个不同的正数
,若有4个不同的正数 满足
满足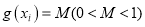 ,且
,且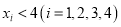 ,则从这四个数中任意选出两个,它们的和不超过5的概率为
,则从这四个数中任意选出两个,它们的和不超过5的概率为A.
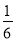 B.
B. 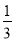 C.
C. 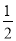 D.
D. 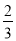
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的年固定成本为250万元,每生产
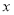 千件,需另投入成本
千件,需另投入成本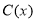 ,当年产量不足80千件时,
,当年产量不足80千件时,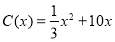 (万元);当年产量不小于80千件时
(万元);当年产量不小于80千件时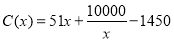 (万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.(1)写出年利润
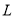 (万元)关于年产量
(万元)关于年产量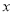 (千件)的函数解析式;
(千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
相关试题

