【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在![]() ,
, ![]() ,
, ![]() 对应的小矩形的面积分别是
对应的小矩形的面积分别是![]() ,且
,且![]() .
.
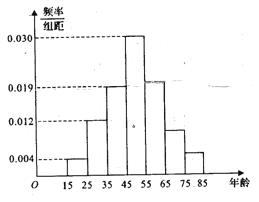
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在![]() 的人数;
的人数;
(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在![]() ,
, ![]() 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在![]() 内的概率.
内的概率.
参考答案:
【答案】(1)![]() ;(2)50;(3)
;(2)50;(3)![]() .
.
【解析】试题分析:(1)利用小矩形面积比就是频率比,和所有频率和为![]() ,可求得各组的频,再利用
,可求得各组的频,再利用![]() 组的频率可估计该地区的人数;(2)由频率分布直方图求平均数可由各组的中间数与该组的频率乘积后再求和可得;(3)先由分层抽样得出抽取
组的频率可估计该地区的人数;(2)由频率分布直方图求平均数可由各组的中间数与该组的频率乘积后再求和可得;(3)先由分层抽样得出抽取![]() 人在各组的分配情况,然后写出所有抽取两人的可能情况,找出满足条件的,利用古典概型可求得结果.
人在各组的分配情况,然后写出所有抽取两人的可能情况,找出满足条件的,利用古典概型可求得结果.
试题解析:(1)设区间![]() 的频率为x,则区间
的频率为x,则区间![]() 内的频率依次为
内的频率依次为![]() ,依题意
,依题意
得![]()
![]()
![]() 在五一活动中消费超过3000元且年龄在
在五一活动中消费超过3000元且年龄在![]() 岁之间的人数为:
岁之间的人数为:
![]() (人)
(人)
(2)依题意,所求的平均数为:
![]() .
.
(3)若按分层抽样,年龄在![]() 分别抽取2人和5人,记年龄在
分别抽取2人和5人,记年龄在![]() 的两
的两
人为A,B,记年龄在![]() 的5人为1,2,3,4,5;随机抽取两人可能情况有:
的5人为1,2,3,4,5;随机抽取两人可能情况有:
(A,B),(A,1)(A,2),(A,3),(A,4),(A,5),(B,1),(B,2),(B,3),(B,4),(B,5),(1,2),(1,3),(1,4)(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共21种情况,
其中满足条件的有:(A,B),(A,1)(A,2),(A,3),(A,4),(A,5),(B,1),(B,2),(B,3),(B,4),(B,5)共11
种故所求概率为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
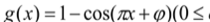 的图象过
的图象过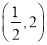 ,若有4个不同的正数
,若有4个不同的正数 满足
满足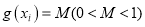 ,且
,且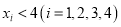 ,则从这四个数中任意选出两个,它们的和不超过5的概率为
,则从这四个数中任意选出两个,它们的和不超过5的概率为A.
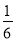 B.
B. 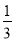 C.
C. 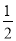 D.
D. 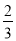
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的年固定成本为250万元,每生产
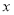 千件,需另投入成本
千件,需另投入成本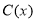 ,当年产量不足80千件时,
,当年产量不足80千件时,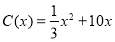 (万元);当年产量不小于80千件时
(万元);当年产量不小于80千件时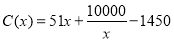 (万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.(1)写出年利润
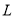 (万元)关于年产量
(万元)关于年产量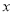 (千件)的函数解析式;
(千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
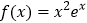 .
.(Ⅰ)求曲线
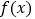 在点
在点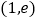 处的切线方程;
处的切线方程;(Ⅱ)若
 对
对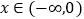 恒成立,求实数
恒成立,求实数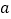 的取值范围;
的取值范围;(Ⅲ)求整数
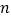 的值,使函数
的值,使函数 在区间
在区间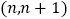 上有零点.
上有零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
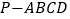 中,底面
中,底面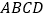 为平行四边形,
为平行四边形, 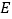 为侧棱
为侧棱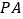 的中点.
的中点.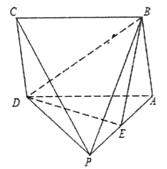
(Ⅰ)求证:
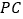 ∥平面
∥平面
(Ⅱ)若
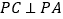 ,
,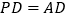 ,
,求证:平面

 平面
平面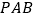
-
科目: 来源: 题型:
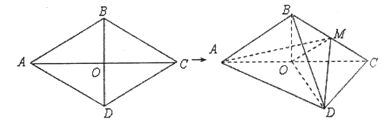
查看答案和解析>>【题目】如图,棱形
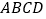 的边长为6,
的边长为6, 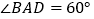 ,
,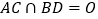 .将棱形
.将棱形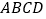 沿对角线
沿对角线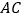 折起,得到三棱锥
折起,得到三棱锥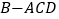 ,点
,点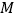 是棱
是棱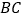 的中点,
的中点, 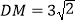 .
.
(Ⅰ)求证:
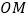 ∥平面
∥平面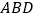 ;
;(Ⅱ)求三棱锥
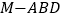 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
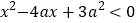 ,其中
,其中 ,命题
,命题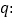 实数
实数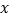 满足
满足|x-3|≤1 .
(1)若
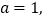 且
且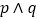 为真,求实数
为真,求实数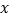 的取值范围;
的取值范围;(2)若
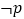 是
是
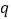 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
相关试题

