【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,
,![]() .
.
(1)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的短轴长为2,过点
的短轴长为2,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
试题分析:(1)由![]() 为等边三角形可得a=2b,又c=1,集合
为等边三角形可得a=2b,又c=1,集合![]() 可求
可求![]() ,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把
,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把
![]() 转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求
转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求
试题解析:(1)![]() 为等边三角形,则
为等边三角形,则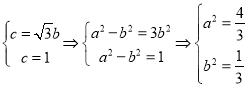 ……2
……2
椭圆![]() 的方程为:
的方程为:![]() ; ……3
; ……3
(2)容易求得椭圆![]() 的方程为
的方程为![]() , ……5
, ……5
当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,不符合题意; ……6
,不符合题意; ……6
当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由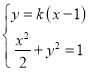 得
得![]() ,设
,设![]() ,
,
则![]() , ……8
, ……8
![]() ∵
∵![]() ,
,
∴![]() ,
,
即![]()
![]() ……10
……10
解得![]() ,即
,即![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]() . ……12
. ……12
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,cos C=.
(1)若·=,求c的最小值;
(2)设向量x=(2sin B,-),y=,且x∥y,求sin(B-A)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知函数
 (其中
(其中 为参数).
为参数).(1)当
 时,证明:
时,证明: 不是奇函数;
不是奇函数;(2)如果
 是奇函数,求实数
是奇函数,求实数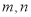 的值;
的值;(3)已知
 ,在(2)的条件下,求不等式
,在(2)的条件下,求不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
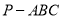 中,平面
中,平面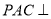 平面
平面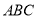 ,
,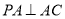 ,
,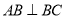 .设
.设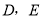 分别为
分别为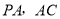 中点.
中点.(1)求证:
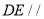 平面
平面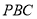 ;
;(2)求证:
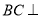 平面
平面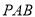 ;
;(3)试问在线段
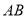 上是否存在点
上是否存在点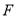 ,使得过三点
,使得过三点 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面 平行?
平行?若存在,指出点
 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
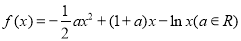 .
.(1)当
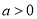 时,求函数
时,求函数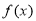 的单调递减区间;
的单调递减区间;(2)当
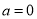 时,设函数
时,设函数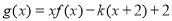 .若函数
.若函数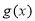 在区间
在区间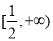 上有两个零点,求实数
上有两个零点,求实数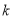 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的两个焦点分别为
的两个焦点分别为 ,
,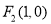 ,短轴的两个端点分别为
,短轴的两个端点分别为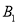 ,
,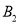 .
.(1)若
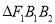 为等边三角形,求椭圆
为等边三角形,求椭圆 的方程;
的方程;(2)若椭圆
 的短轴长为2,过点
的短轴长为2,过点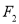 的直线
的直线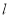 与椭圆
与椭圆 相交于
相交于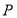 、
、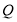 两点,且
两点,且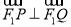 ,求直线
,求直线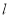 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为
 ,求
,求 ,并估计
,并估计 的预报值;
的预报值; (Ⅱ)现准备勘探新井
 ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的 的值(
的值( 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井 ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?(参考公式和计算结果:
 )
)(Ⅲ)设出油量与勘探深度的比值
 不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
相关试题

