【题目】在△ABC中,角A,B,C的对边分别为a,b,c,cos C=.
(1)若·=,求c的最小值;
(2)设向量x=(2sin B,-),y=,且x∥y,求sin(B-A)的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用向量的数量积公式及余弦定理求解;(2)借助题设运用向量平行建立方程,再利用三角变换公式探求.
试题解析:
(1) ∵ ·=![]() ,∴ abcosC=
,∴ abcosC=![]() ,∴ ab=15…………………..3分
,∴ ab=15…………………..3分
∴ c2=a2+b2-2abcosC≥2ab-2ab·![]() =21(当且仅当a=b时取等号).
=21(当且仅当a=b时取等号).
∵ c>0,∴ c≥![]() ,…………………………………………………………..5分
,…………………………………………………………..5分
∴ c的最小值为![]() …………………………………………………….7分
…………………………………………………….7分
(2) ∵ x∥y,∴ 2sin B![]() +
+![]() cos2B=0,
cos2B=0,
2sinBcosB+![]() cos2B=0,即sin 2B+
cos2B=0,即sin 2B+![]() cos2B=0,
cos2B=0,
∴ tan2B=-![]() ,∴ 2B=
,∴ 2B=![]() 或
或![]() ,∴ B=
,∴ B=![]() 或
或![]() ……………………10分
……………………10分
∵ cos C=![]() <
<![]() ,∴ C>
,∴ C>![]() ,
,
∴ B=![]() (舍去),∴ B=
(舍去),∴ B=![]() ……………………………………………..12分
……………………………………………..12分
∴ sin(B-A)=sin[B-(π-B-C)]
=sin![]() =sinCcos
=sinCcos![]() -cos Csin
-cos Csin![]()
=![]() ×
×![]() -
-![]() ×
×![]() =
=![]() …………………………………………..16分
…………………………………………..16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin
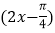 -2
-2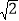 ·sin2x.
·sin2x.(1) 求函数f(x)的最小正周期;
(2) 求函数f(x)图象的对称轴方程、对称中心的坐标;
(3) 当0≤x≤
 时,求函数f(x)的最大、最小值.
时,求函数f(x)的最大、最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
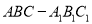 中,底面
中,底面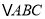 是边长为2的等边三角形,
是边长为2的等边三角形,  为
为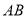 的中点.
的中点.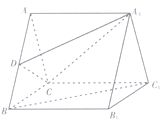
(1)求证:
 平面
平面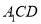 ;
;(2)若四边形
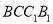 是正方形,且
是正方形,且 ,求直线
,求直线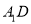 与平面
与平面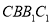 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为原点,A,B,C为平面内的三点.求证:
(1) 若A,B,C三点共线,则存在实数α,β,且α+β=1,
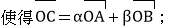
(2) 若存在实数α,β,且α+β=1,使得
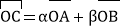 ,则A,B,C三点共线.
,则A,B,C三点共线. -
科目: 来源: 题型:
查看答案和解析>>【题目】 已知函数
 (其中
(其中 为参数).
为参数).(1)当
 时,证明:
时,证明: 不是奇函数;
不是奇函数;(2)如果
 是奇函数,求实数
是奇函数,求实数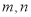 的值;
的值;(3)已知
 ,在(2)的条件下,求不等式
,在(2)的条件下,求不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
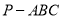 中,平面
中,平面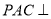 平面
平面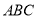 ,
,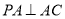 ,
,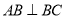 .设
.设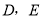 分别为
分别为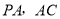 中点.
中点.(1)求证:
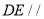 平面
平面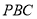 ;
;(2)求证:
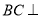 平面
平面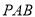 ;
;(3)试问在线段
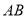 上是否存在点
上是否存在点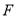 ,使得过三点
,使得过三点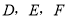 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面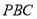 平行?
平行?若存在,指出点
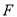 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
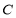 的两个焦点分别为
的两个焦点分别为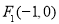 ,
,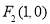 ,短轴的两个端点分别为
,短轴的两个端点分别为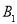 ,
,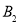 .
.(1)若
 为等边三角形,求椭圆
为等边三角形,求椭圆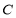 的方程;
的方程;(2)若椭圆
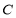 的短轴长为2,过点
的短轴长为2,过点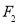 的直线
的直线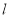 与椭圆
与椭圆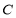 相交于
相交于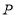 、
、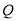 两点,且
两点,且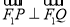 ,求直线
,求直线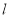 的方程.
的方程.
相关试题

