【题目】已知一个口袋有m个白球,n个黑球(m,n![]()
![]() ,n
,n![]() 2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
![]()
(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明 ![]()
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据条件先确定总事件数为![]() ,而编号为2的抽屉内放的是黑球的事件数为
,而编号为2的抽屉内放的是黑球的事件数为![]() ,最后根据古典概型的概率公式即可求概率;(2)先确定最后一个取出的黑球所在抽屉编号的倒数为
,最后根据古典概型的概率公式即可求概率;(2)先确定最后一个取出的黑球所在抽屉编号的倒数为![]() ,所对应的概率
,所对应的概率![]() ,再根据数学期望公式得
,再根据数学期望公式得![]() ,利用性质
,利用性质![]() ,进行放缩变形:
,进行放缩变形: ![]() ,最后利用组合数性质
,最后利用组合数性质![]() 化简,可得结论.
化简,可得结论.
试题解析:解:(1)编号为2的抽屉内放的是黑球的概率![]() 为:
为: ![]() .
.
(2)随机变量X的概率分布为:
X |
|
|
| … |
| … |
|
P |
|
|
| … |
| … |
|
随机变量X的期望为:
![]() .
.
所以![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
点睛:求解离散型随机变量的数学期望的一般步骤为:
(1)“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
(2)“探求概率”,即利用排列组合、枚举法、概率公式(常见的有古典概型公式、几何概型公式、互斥事件的概率和公式、独立事件的概率积公式,以及对立事件的概率公式等),求出随机变量取每个值时的概率;
(3)“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
(4)“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值,对于有些实际问题中的随机变量,如果能够断定它服从某常见的典型分布(如二项分布![]() ),则此随机变量的期望可直接利用这种典型分布的期望公式(
),则此随机变量的期望可直接利用这种典型分布的期望公式(![]() )求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.
)求得.因此,应熟记常见的典型分布的期望公式,可加快解题速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:y=cos x,C2:y=sin (2x+
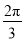 ),则下面结论正确的是
),则下面结论正确的是A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
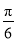 个单位长度,得到曲线C2
个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
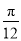 个单位长度,得到曲线C2
个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的
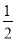 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移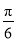 个单位长度,得到曲线C2
个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的
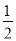 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移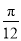 个单位长度,得到曲线C2
个单位长度,得到曲线C2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且
 .
.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
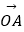 =(4,3),
=(4,3), 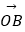 =(2,﹣1),O为坐标原点,P是直线AB上一点.
=(2,﹣1),O为坐标原点,P是直线AB上一点.
(1)若点P是线段AB的中点,求向量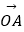 与向量
与向量 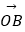 夹角θ的余弦值;
夹角θ的余弦值;
(2)若点P在线段AB的延长线上,且|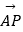 |=
|=  |
| 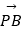 |,求点P的坐标.
|,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥中P﹣ABCD,底面ABCD为边长为
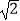 的正方形,PA⊥BD.
的正方形,PA⊥BD. 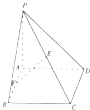
(1)求证:PB=PD;
(2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是各项都为正数的等比数列,其前n项和为Sn , 且S2=3,S4=15.
(1)求数列{an}的通项公式;
(2)若数列{bn}是等差数列,且b3=a3 , b5=a5 , 试求数列{bn}的前n项和Mn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
 AA1 , D是棱AA1的中点.
AA1 , D是棱AA1的中点.
(Ⅰ)证明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.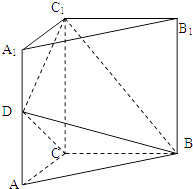
相关试题

