【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= ![]() AA1 , D是棱AA1的中点.
AA1 , D是棱AA1的中点.
(Ⅰ)证明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.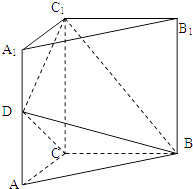
参考答案:
【答案】证明:(Ⅰ)由题意知BC⊥CC1 , BC⊥AC,CC1∩AC=C,
∴BC⊥平面ACC1A1 , 又DC1平面ACC1A1 ,
∴DC1⊥BC.
由题设知∠A1DC1=∠ADC=45°,
∴∠CDC1=90°,即DC1⊥DC,又DC∩BC=C,
∴DC1⊥平面BDC,又DC1平面BDC1 ,
∴平面BDC1⊥平面BDC;
(Ⅱ)设棱锥B﹣DACC1的体积为V1 , AC=1,由题意得V1= ![]() ×
× ![]() ×1×1=
×1×1= ![]() ,
,
又三棱柱ABC﹣A1B1C1的体积V=1,
∴(V﹣V1):V1=1:1,
∴平面BDC1分此棱柱两部分体积的比为1:1.
【解析】(Ⅰ)由题意易证DC1⊥平面BDC,再由面面垂直的判定定理即可证得平面BDC1⊥平面BDC;(Ⅱ)设棱锥B﹣DACC1的体积为V1 , AC=1,易求V1= ![]() ×
× ![]() ×1×1=
×1×1= ![]() ,三棱柱ABC﹣A1B1C1的体积V=1,于是可得(V﹣V1):V1=1:1,从而可得答案.
,三棱柱ABC﹣A1B1C1的体积V=1,于是可得(V﹣V1):V1=1:1,从而可得答案.
【考点精析】本题主要考查了棱柱的结构特征和平面与平面垂直的判定的相关知识点,需要掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个口袋有m个白球,n个黑球(m,n

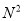 ,n
,n 2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥中P﹣ABCD,底面ABCD为边长为
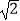 的正方形,PA⊥BD.
的正方形,PA⊥BD. 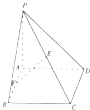
(1)求证:PB=PD;
(2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是各项都为正数的等比数列,其前n项和为Sn , 且S2=3,S4=15.
(1)求数列{an}的通项公式;
(2)若数列{bn}是等差数列,且b3=a3 , b5=a5 , 试求数列{bn}的前n项和Mn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
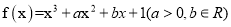 有极值,且导函数
有极值,且导函数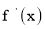 的极值点是
的极值点是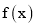 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若
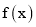 ,
, 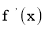 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于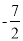 ,求a的取值范围。
,求a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四点F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求证:平面CBE⊥平面EDB;
(Ⅲ)当x=2时,求二面角F﹣EB﹣C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
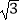 ,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
(Ⅰ)求证:PH∥平面GED;
(Ⅱ)过点F作平面α,使ED∥平面α,当平面α⊥平面EDG时,设PA与平面α交于点Q,求PQ的长.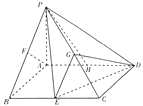
相关试题

