【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3, ![]() ),点B的极坐标为(6,
),点B的极坐标为(6, ![]() ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
参考答案:
【答案】
(1)解:A、B的直角坐标分别是A(0,3),B(3 ![]() ,3),
,3),
故直线AB的极坐标方程是ρsinθ=3,
曲线C化为极坐标为ρ=2cosθ
(2)解:设射线l:θ=α,代入曲线C得:ρM=2cosα,
代入直线AB得:ρM= ![]() ,
,
依题意得 ![]() 2cosα=2,解得:tanα=3.
2cosα=2,解得:tanα=3.
所以射线l所在直线的直角坐标方程为:y=3x
【解析】(1)求出A、B的直角坐标,求出直线AB的极坐标方程,根y=ρsinα,x=ρcosθ求出C的极坐标方程即可;(2)设射线l:θ=α,分别代入曲线C的方程和直线AB的方程,得到关于α的方程,求出tanα的值,从而求出答案.
【考点精析】本题主要考查了一般式方程的相关知识点,需要掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0)才能正确解答此题.
(A,B不同时为0)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:圆心到直线的距离与圆的半径之比为直线关于圆的距离比
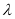 .
.(1)设圆
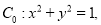 求过
求过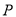 (2,0)的直线关于圆
(2,0)的直线关于圆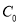 的距离比
的距离比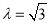 的直线方程;
的直线方程;(2)若圆
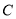 与
与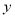 轴相切于点
轴相切于点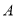 (0,3)且直线
(0,3)且直线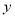 =
= 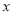 关于圆
关于圆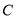 的距离比
的距离比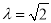 ,求此圆的
,求此圆的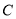 的方程;
的方程;(3)是否存在点
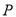 ,使过
,使过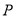 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆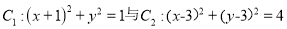 的距离比始终相等?若存在,求出相应的点
的距离比始终相等?若存在,求出相应的点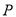 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,设倾斜角为
中,设倾斜角为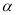 的直线
的直线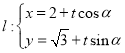 (
(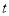 为参数)与曲线
为参数)与曲线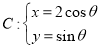 (
(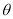 为参数)相交于不同的两点
为参数)相交于不同的两点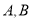 .
.(1)若
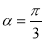 ,求线段
,求线段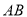 中点
中点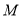 的坐标;
的坐标;(2)若
 ,其中
,其中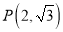 ,求直线
,求直线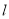 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
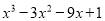 (x
(x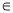 R),g(x)=2a-1
R),g(x)=2a-1(1)求函数f(x)的单调区间与极值.
(2)若f(x)≥g(x)对
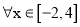 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱
 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,
, 为棱
为棱 上的点.
上的点.(1)证明:
 ;
;(2)是否存在一点
 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,前n项和为Sn , 且Sn=
 ,数列{bn}的前n项和为Tn , 且bn=
,数列{bn}的前n项和为Tn , 且bn= 
(1)求数列{an}的通项公式;
(2)是否存在m,n∈N* , 使得Tn=am , 若存在,求出所有满足题意的m,n,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一动圆与圆
 外切,与圆
外切,与圆 内切.
内切.(1)求动圆圆心
 的轨迹
的轨迹 的方程.
的方程.(2)设过圆心
 的直线
的直线 与轨迹
与轨迹 相交于
相交于 两点,
两点, (
( 为圆
为圆 的圆心)的内切圆
的圆心)的内切圆 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
相关试题

