【题目】已知等差数列![]() 满足
满足![]() ,前8项和
,前8项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() .
.
① 证明:![]() 为等比数列;
为等比数列;
② 求集合![]() .
.
参考答案:
【答案】(1)![]() (2)①见解析,②
(2)①见解析,②![]()
![]()
【解析】
(1)设等差数列{an}的公差为d.根据a4=4,前8项和S8=36.可得数列{an}的通项公式;
(2)①设数列{bn}前n项的和为Bn.根据bn=Bn﹣Bn﹣1,数列{bn}满足![]() .建立关系即可求解;
.建立关系即可求解;
②由![]() ,得
,得![]() ,即
,即![]() .记
.记![]() ,由①得,
,由①得,![]() ,
,
由![]() ,得cm=3cp>cp,所以m<p;设t=p﹣m(m,p,t∈N*),由
,得cm=3cp>cp,所以m<p;设t=p﹣m(m,p,t∈N*),由![]() ,得
,得![]() .讨论整数成立情况即可;
.讨论整数成立情况即可;
(1)设等差数列![]() 的公差为d.
的公差为d.
因为等差数列![]() 满足
满足![]() ,前8项和
,前8项和![]() ,
,
所以 ,解得
,解得![]()
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)①设数列![]() 前
前![]() 项的和为
项的和为![]() .
.
![]()
得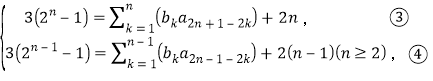
由③-④得
3![]()
-![]()
=![]()
-![]()
![]() .
.
所以![]()
![]() ,
,
又![]() ,所以
,所以![]() ,满足上式.
,满足上式.
所以![]()
当![]() 时,
时,![]()
由⑤-⑥得,![]() .
.
![]()
![]() ,
,
所以![]() ,
,![]() ,
,
所以数列![]() 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.
②由![]() ,得
,得![]() ,即
,即![]() .
.
记![]() ,由①得,
,由①得,![]() ,
,
所以![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立).
时等号成立).
由![]() ,得
,得![]() ,
,
所以![]() .
.
设![]()
![]() ,由
,由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,此时
,此时![]() 符合题意;
符合题意;
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,不合题意.
,不合题意.
下面证明当![]() 时,
时,![]() .
.
不妨设![]()
![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上单调增函数,
上单调增函数,
所以![]() ,
,
所以当![]() 时,
时,![]() ,不合题意.
,不合题意.
综上,所求集合![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆
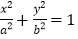
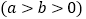 的左焦点为
的左焦点为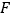 ,右顶点为
,右顶点为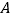 ,上顶点为
,上顶点为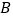 .
.(1)已知椭圆的离心率为
 ,线段
,线段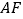 中点的横坐标为
中点的横坐标为 ,求椭圆的标准方程;
,求椭圆的标准方程;(2)已知△
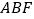 外接圆的圆心在直线
外接圆的圆心在直线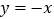 上,求椭圆的离心率
上,求椭圆的离心率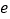 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一艺术拱门由两部分组成,下部为矩形
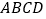 ,
,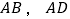 的长分别为
的长分别为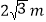 和
和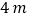 ,上部是圆心为
,上部是圆心为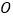 的劣弧
的劣弧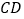 ,
, .
.
(1)求图1中拱门最高点到地面的距离;
(2)现欲以B点为支点将拱门放倒,放倒过程中矩形
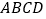 所在的平面始终与地面垂直,如图2、图3、图4所示.设
所在的平面始终与地面垂直,如图2、图3、图4所示.设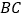 与地面水平线
与地面水平线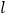 所成的角为
所成的角为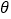 .记拱门上的点到地面的最大距离为
.记拱门上的点到地面的最大距离为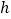 ,试用
,试用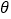 的函数表示
的函数表示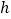 ,并求出
,并求出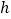 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论
 的单调性;
的单调性;(2)设
 的导函数为
的导函数为 ,若
,若 有两个不相同的零点
有两个不相同的零点 .
.① 求实数
 的取值范围;
的取值范围;② 证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】由数字1,2,3,4,5,6组成没有重复数字的三位数,偶数共有______个,其中个位数字比十位数字大的偶数共有______个.
相关试题

