【题目】已知曲线方程C:.
(1)当![]() 时,求圆心和半径;
时,求圆心和半径;
(2)若曲线C表示的圆与直线l: ![]() 相交于M,N,且
相交于M,N,且![]() ,求m的值.
,求m的值.
参考答案:
【答案】(1)圆心坐标为(1,2),半径为![]() ;(2)m=4.
;(2)m=4.
【解析】试题分析: (1)当m=﹣6时,方程C:x2+y2﹣2x﹣4y+m=0,可化为(x﹣1)2+(y﹣2)2=11,即可求得圆心和半径;
(2)利用圆心(1,2)到直线l:x+2y﹣4=0的距离公式可求得圆心到直线距离d,利用圆的半径、弦长之半、d构成的直角三角形即可求得m的值.
试题解析:
(1)当m=﹣6时,方程C:x2+y2﹣2x﹣4y+m=0,可化为(x﹣1)2+(y﹣2)2=11,
圆心坐标为(1,2),半径为![]() ;
;
(2)∵(x﹣1)2+(y﹣2)2=5﹣m,
∴圆心(1,2)到直线l:x+2y﹣4=0的距离d=![]() ,
,
又圆(x﹣1)2+(y﹣2)2=5﹣m的半径r=![]() ,
,![]() ,
,
∴(![]() )2+(
)2+(![]() )2=5﹣m,得m=4.
)2=5﹣m,得m=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )

A.56
B.60
C.120
D.140 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M:x2+y2﹣2ay=0(a>0)截直线x+y=0所得线段的长度是2
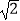 ,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
A.内切
B.相交
C.外切
D.相离 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>
 时,f(x+
时,f(x+  )=f(x﹣
)=f(x﹣  ).则f(6)=( )
).则f(6)=( )
A.﹣2
B.﹣1
C.0
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx
B.y=lnx
C.y=ex
D.y=x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用
 与保护罩容积
与保护罩容积 之间的函数关系式;
之间的函数关系式;(Ⅱ)求该博物馆支付总费用的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=
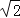 ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.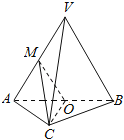
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
相关试题

