【题目】已知椭圆：的离心率为，且过点，椭圆的右顶点为，点的坐标为．

（1）求椭圆的方程；

（2）已知纵坐标不同的两点，为椭圆上的两个点，且，，三点共线，线段的中点为，求直线的斜率的取值范围．

【答案】（1）；（2）.

【解析】

（1）由题意结合椭圆的性质可得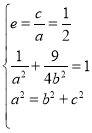，求得、即可得解；

（2）由题意设直线方程为，点，，，直线的斜率为，联立方程结合韦达定理可表示出点的坐标，进而可得，结合基本不等式即可得解.

（1）∵椭圆：的离心率为，且过点，

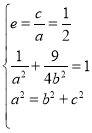∴，解得，，

∴椭圆的方程为；

（2）依题意知直线过点，且斜率不为0，

故可设其方程为，

由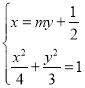，消去得，，

设点，，，直线的斜率为，

故，∴，∴，

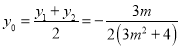又点的坐标为，∴，

当时，；

当时，，

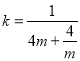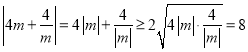∵，当且仅当时，等号成立，

∴，∴，

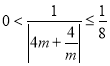∴且；

综上所述，直线的斜率的取值范围是．

关闭