【题目】已知函数![]() .
.
(Ⅰ)证明: 当![]() 时,
时, ![]() .
.
(Ⅱ)证明: 当![]() 时,
时, ![]() .
.
参考答案:
【答案】(1)详见解析;(Ⅱ)详见解析.
【解析】试题分析:
(Ⅰ)由不等式的特征构造函数![]() ,结合函数的单调性求得函数的最大值,据此即可证得题中的结论:
,结合函数的单调性求得函数的最大值,据此即可证得题中的结论: ![]() .
.
(Ⅱ)结合(I)的结论构造函数![]() ,研究该函数的性质即可证得当
,研究该函数的性质即可证得当![]() 时,
时, ![]() .
.
试题解析:
(Ⅰ)证明: 要证![]() , 也即证
, 也即证![]() .
.
令![]() , 则
, 则![]() . 令
. 令![]() , 则
, 则![]() . 因此, 当
. 因此, 当![]() 时, 有
时, 有![]() , 故
, 故![]() 在
在![]() 上单调递减; 当
上单调递减; 当![]() 时, 有
时, 有![]() , 故
, 故![]() 在
在![]() 上单调递增.
上单调递增.
所以, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
又![]() ,
, ![]() . 故
. 故![]() 成立, 即
成立, 即![]() 成立. 原命题得证.
成立. 原命题得证.
(Ⅱ) 证明: 由 (I) 得: 当![]() 时,
时, ![]()
令![]() , 则
, 则
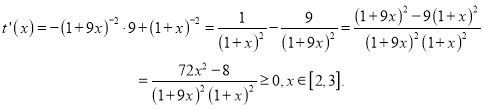
所以, ![]() 在
在![]() 上单调递增,即
上单调递增,即![]()
所以![]()
![]() 得证.
得证.
下证![]() .
.
即证![]()
令![]() 则
则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以, ![]() ,得证.
,得证.
另证:要证![]() ,即证
,即证![]() ,
,
令![]() 在
在![]() 上递增,所以
上递增,所以![]() 得证.
得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
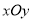 中,已知椭圆
中,已知椭圆 (
(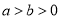 ),圆
),圆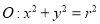 (
(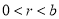 ),若圆
),若圆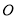 的一条切线
的一条切线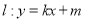 与椭圆
与椭圆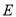 相交于
相交于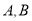 两点.
两点.(1)当
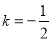 ,
, 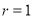 时,若点
时,若点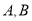 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆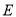 的方程;
的方程;(2)若以
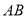 为直径的圆经过坐标原点
为直径的圆经过坐标原点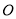 ,探究
,探究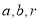 之间的等量关系,并说明理由.
之间的等量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
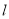 的参数方程为
的参数方程为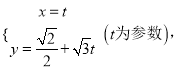 若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为
若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为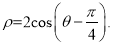
(1)求直线
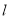 的斜率和曲线C的直角坐标方程;
的斜率和曲线C的直角坐标方程;(2)若直线
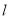 与曲线C交于A、B 两点,设点
与曲线C交于A、B 两点,设点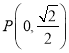 ,求|PA|+|PB|.
,求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex+ax-a(a∈R且a≠0)在点
 处的切线
处的切线与直线
 平行, (1)求实数a的值,
平行, (1)求实数a的值,(2)求此时f(x)在[-2,1]上的最大、最小值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】设甲、乙、丙3个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这3个协会中抽取6名运动员组队参加比赛.
(1)求应从这3个协会中分别抽取的运动员的人数.
(2)将抽取的6名运动员进行编号,编号分别为A1,A2,A3,A4,A5,A6.现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设事件A为“编号为A5和A6的2名运动员中至少有1人被抽到”,求事件A发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
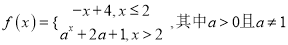 .若
.若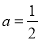 时方程
时方程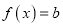 有两 个不同的实根,则实数
有两 个不同的实根,则实数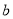 的取值范围是________;若
的取值范围是________;若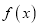 的值域为
的值域为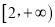 ,则实数
,则实数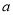 的
的 取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求与直线3x-4y+7=0平行,且在两坐标轴上截距之和为1的直线l的方程.
相关试题

