【题目】设甲、乙、丙3个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这3个协会中抽取6名运动员组队参加比赛.
(1)求应从这3个协会中分别抽取的运动员的人数.
(2)将抽取的6名运动员进行编号,编号分别为A1,A2,A3,A4,A5,A6.现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设事件A为“编号为A5和A6的2名运动员中至少有1人被抽到”,求事件A发生的概率.
参考答案:
【答案】(1) 从甲、乙、丙三个协会中抽取的运动员人数分别为3,1,2;(2)①见解析;②![]() .
.
【解析】试题分析:(1)由题为分层抽样,可知每个个体被抽到的可能性相同.则可得概率为![]() ;
;
(2)(i)用所给编号列出所有可能的结果则为6个元素中取出2个的所有情况可列出;
(ii)为古典概型,可结合上问中的结论,确定所包含的基本事件,代入古典概率公式可得。
试题解析:(Ⅰ)分层抽样中,每个个体被抽到的可能性相同
乙乒乓球协会的某运动员被抽到的概率![]()
(Ⅱ)(i)从6名运动员中随机抽取2名的所有结果为:
(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),
(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A3,A4),
(A3,A5),(A3,A6),(A4,A5),(A4,A6)),(A5,A6),共15种;
(ii)设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”,
则事件A包含:(A1,A5),(A1,A6),(A2,A5),(A2,A6),
(A3,A5),(A3,A6),(A4,A5),(A4,A6)),(A5,A6)共9个基本事件,
∴事件A发生的概率P=![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
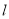 的参数方程为
的参数方程为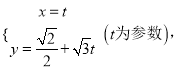 若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为
若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为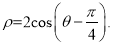
(1)求直线
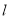 的斜率和曲线C的直角坐标方程;
的斜率和曲线C的直角坐标方程;(2)若直线
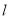 与曲线C交于A、B 两点,设点
与曲线C交于A、B 两点,设点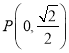 ,求|PA|+|PB|.
,求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex+ax-a(a∈R且a≠0)在点
 处的切线
处的切线与直线
 平行, (1)求实数a的值,
平行, (1)求实数a的值,(2)求此时f(x)在[-2,1]上的最大、最小值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
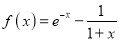 .
.(Ⅰ)证明: 当
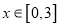 时,
时, 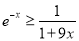 .
.(Ⅱ)证明: 当
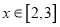 时,
时, 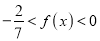 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
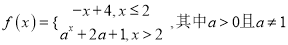 .若
.若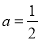 时方程
时方程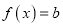 有两 个不同的实根,则实数
有两 个不同的实根,则实数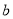 的取值范围是________;若
的取值范围是________;若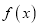 的值域为
的值域为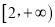 ,则实数
,则实数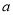 的
的 取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求与直线3x-4y+7=0平行,且在两坐标轴上截距之和为1的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为________.
相关试题

