【题目】“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801﹣2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
等级 | P1 | P2 | P3 | P4 |
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
参考答案:
【答案】解:(Ⅰ)∵在(4,6]之间的数据一共有6个,
再由频布直方图得:落在(4,6]之间的频率为0.03×2=0.06,
∴n= ![]() =100,
=100,
由频率分布直方图的性质得:
(0.03+x+0.12+0.14+0.15)×2=1,
解得x=0.06.
(Ⅱ)由频率分布直方图可知:落在(6,8]之间共:0.12×2×100=24台,
又∵在(5,6]之间共4台,
∴落在(5,8]之间共28台,
∴估计这批空气净化器(共2000台)中等级为P2的空气净化器有560台.
(Ⅲ)设“恰好有1台等级为P2”为事件B,
依题意落在(4,6]之间共6台,属于国标P2级的有4台,
则从(4,6]中随机抽取2台,基本事件总数n= ![]() ,
,
事件B包含的基本事件个数m= ![]() =8,
=8,
∴恰好有1台等级为P2的概率P(B)= ![]()
【解析】(Ⅰ)先求出在(4,6]之间的数据一共有6个,再由频布直方图得:落在(4,6]之间的频率为0.03×2=0.06,由此能求出n的值及频率分布直方图中的x值.(Ⅱ)由频率分布直方图可知:落在(6,8]之间共24台,在(5,6]之间共4台,从而落在(5,8]之间共28台,由此能估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台.(Ⅲ)设“恰好有1台等级为P2”为事件B,依题意落在(4,6]之间共6台,属于国标P2级的有4台,则从(4,6]中随机抽取2台,基本事件总数n= ![]() ,事件B包含的基本事件个数m=
,事件B包含的基本事件个数m= ![]() =8,由此能求出恰好有1台等级为P2的概率.
=8,由此能求出恰好有1台等级为P2的概率.
【考点精析】通过灵活运用频率分布直方图,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)=
 (|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
(|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;
④设曲线y=ex(e是自然对数的底数)上不同两点A(x1 , y1),B(x2 , y2),则φ(A,B)<1.
其中真命题的序号为 . (将所有真命题的序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 将
将 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数 的图象.
的图象.(1)求函数
 的解析式;
的解析式;(2)若方程
 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求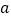 的取值范围;
的取值范围;(3)若函数
 与
与 的图象关于直线
的图象关于直线 对称,设
对称,设 ,已知
,已知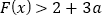 对任意的
对任意的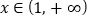 恒成立,求
恒成立,求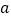 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中,a1=1,an+1=
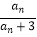 (n∈N*).
(n∈N*).
(1)求证:{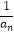 +
+  }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
, )的一系列对应值如表:
)的一系列对应值如表:
(1)根据表格提供的数据求函数
 的一个解析式;
的一个解析式;(2)根据(1)的结果:
①当
 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围;
的取值范围;②若
 ,
, 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较 与
与 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
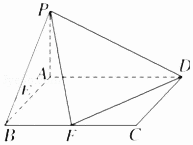
(1)证明:PF⊥FD;
(2)若PA=1,求点E到平面PFD的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆M恒过点(0,1),且与直线y=﹣1相切.
(1)求圆心M的轨迹方程;
(2)动直线l过点P(0,﹣2),且与点M的轨迹交于A、B两点,点C与点B关于y轴对称,求证:直线AC恒过定点.
相关试题

