【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点. 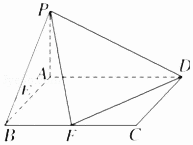
(1)证明:PF⊥FD;
(2)若PA=1,求点E到平面PFD的距离.
参考答案:
【答案】
(1)证明:连接AF,则AF= ![]() ,DF=
,DF= ![]() ,
,
又AD=2,∴DF2+AF2=AD2,∴DF⊥AF,
又PA⊥平面ABCD,∴DF⊥PA,又PA∩AF=A,
∴DF⊥平面PAF,
又PF平面PAF,
∴DF⊥PF.
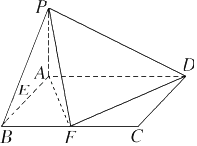
(2)解:∵S△EFD=2﹣ ![]() =
= ![]() ,
,
∴VP﹣EFD= ![]() =
= ![]() ,
,
∵VE﹣PFD=VP﹣AFD,
∴ ![]() ,解得h=
,解得h= ![]() ,即点E到平面PFD的距离为
,即点E到平面PFD的距离为 ![]() .
.
【解析】(1)连接AF,通过计算利用勾股定理证明DF⊥AF,证明DF⊥PA,推出DF⊥平面PAF,然后证明DF⊥PF.(2)利用等体积方法,求点E到平面PFD的距离.
【考点精析】通过灵活运用直线与平面垂直的性质,掌握垂直于同一个平面的两条直线平行即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中,a1=1,an+1=
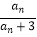 (n∈N*).
(n∈N*).
(1)求证:{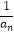 +
+  }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801﹣2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
累积净化量(克)
(3,5]
(5,8]
(8,12]
12以上
等级
P1
P2
P3
P4
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
, )的一系列对应值如表:
)的一系列对应值如表:
(1)根据表格提供的数据求函数
 的一个解析式;
的一个解析式;(2)根据(1)的结果:
①当
 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围;
的取值范围;②若
 ,
, 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较 与
与 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆M恒过点(0,1),且与直线y=﹣1相切.
(1)求圆心M的轨迹方程;
(2)动直线l过点P(0,﹣2),且与点M的轨迹交于A、B两点,点C与点B关于y轴对称,求证:直线AC恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=lnx+
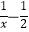 ,g(x)=ex﹣
,g(x)=ex﹣ 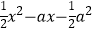 (e是自然对数的底数,a∈R).
(e是自然对数的底数,a∈R).
(Ⅰ)求证:|f(x)|≥﹣(x﹣1)2+ ;
;
(Ⅱ)已知[x]表示不超过x的最大整数,如[1.9]=1,[﹣2.1]=﹣3,若对任意x1≥0,都存在x2>0,使得g(x1)≥[f(x2)]成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
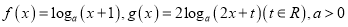 且
且 .
.(Ⅰ) 若1是关于x的方程
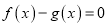 的一个解,求t的值;
的一个解,求t的值;(Ⅱ) 当
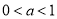 且
且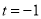 时,解不等式
时,解不等式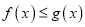 ;
;(Ⅲ)若函数
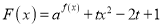 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
相关试题

