【题目】已知函数![]() 将
将![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(Ⅰ)由图象的平移可得g(x)的解析式;
(Ⅱ)设![]() ,问题转化为
,问题转化为![]() 在t∈[1,2]上有且仅有一个实根,通过分类讨论的思想得到结果;
在t∈[1,2]上有且仅有一个实根,通过分类讨论的思想得到结果;
(Ⅲ)设![]() ,t∈(2,+∞).问题转化为t2﹣4at+4a>0对任意t∈(2,+∞)恒成立,变量分离后构造函数
,t∈(2,+∞).问题转化为t2﹣4at+4a>0对任意t∈(2,+∞)恒成立,变量分离后构造函数![]() ,可得其最小值,进而可得答案.
,可得其最小值,进而可得答案.
试题解析:
(1) ![]()
(2)设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]()
于是只须![]() 在
在![]() 上有且仅有一个实根,
上有且仅有一个实根,
法1:设![]() ,对称轴t=
,对称轴t=![]() ,则
,则![]() ① , 或
① , 或 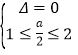 ②
②
由①得 ![]() ,即
,即![]() ,
, ![]()
由②得![]() 无解, ,则
无解, ,则![]() 。
。
法2:由![]() ,得,
,得, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,记
,记![]() ,
,
则![]() 在
在![]() 上是单调函数,因为故要使题设成立,
上是单调函数,因为故要使题设成立,
只须![]() ,即
,即![]() ,
,
从而有![]()
(3)设![]() 的图像上一点
的图像上一点![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
由点![]() 在
在![]() 的图像上,所以
的图像上,所以![]() ,
,
于是![]() 即
即![]() .
. ![]() .
.
由![]() ,化简得
,化简得![]() ,设
,设![]() ,即
,即![]() 恒成立.
恒成立.
注意到t﹣1>1,分离参数得![]() 对任意t∈(2,+∞)恒成立.
对任意t∈(2,+∞)恒成立.
设![]() , t∈(2,+∞),即
, t∈(2,+∞),即![]()
而![]() .
.
可证m(t)在(2,+∞)上单调递增.
∴m(t)>m(2)=4,
∴![]() ,即a∈(﹣∞,1].
,即a∈(﹣∞,1].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中, a、b、c分别为角A、B、C的对边,且
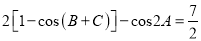
(1)若
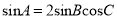 ,试判断△ABC的形状;
,试判断△ABC的形状;(2)若a=
 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设
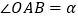 .(注:底面直径和高相等的圆柱叫做等边圆柱.)
.(注:底面直径和高相等的圆柱叫做等边圆柱.)(1)用
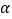 表示圆柱的高;
表示圆柱的高;(2)实践表明,当球心
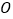 和圆柱底面圆周上的点
和圆柱底面圆周上的点 的距离达到最大时,景观的观赏效
的距离达到最大时,景观的观赏效果最佳,求此时
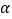 的值.
的值.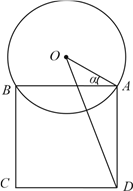
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)=
 (|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
(|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;
④设曲线y=ex(e是自然对数的底数)上不同两点A(x1 , y1),B(x2 , y2),则φ(A,B)<1.
其中真命题的序号为 . (将所有真命题的序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中,a1=1,an+1=
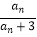 (n∈N*).
(n∈N*).
(1)求证:{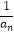 +
+  }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801﹣2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
累积净化量(克)
(3,5]
(5,8]
(8,12]
12以上
等级
P1
P2
P3
P4
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
, )的一系列对应值如表:
)的一系列对应值如表:
(1)根据表格提供的数据求函数
 的一个解析式;
的一个解析式;(2)根据(1)的结果:
①当
 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围;
的取值范围;②若
 ,
, 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较 与
与 的大小.
的大小.
相关试题

