【题目】写出与α=-1910°终边相同的角的集合,并把集合中适合不等式-720°≤β<360°的元素β写出来.
参考答案:
【答案】{β|β=k·360°-1 910°,k∈Z};元素β见解析
【解析】
把α=-1 910°加上![]() 可得与α=-1 910°终边相同的角的集合,分别取k=4,5,6,求得适合不等式-720°≤β<360°的元素β.
可得与α=-1 910°终边相同的角的集合,分别取k=4,5,6,求得适合不等式-720°≤β<360°的元素β.
与α=-1 910°终边相同的角的集合为{β|β=k·360°-1910°,k∈Z}.
∵-720°≤β<360°,即-720°≤k·360°-1 910°<360°(k∈Z),∴![]() (k∈Z),故取k=4,5,6.
(k∈Z),故取k=4,5,6.
k=4时,β=4×360°-1910°=-470°;
k=5时,β=5×360°-1910°=-110°;
k=6时,β=6×360°-1910°=250°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列各式的符号:
①sin 145°cos(-210°);②sin 3·cos 4·tan 5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角
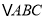 中,
中, 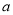 、
、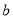 、
、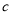 分别为角
分别为角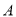 、
、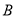 、
、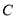 所对的边,且
所对的边,且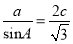 .
.(
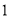 )确定角
)确定角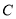 的大小.
的大小.(
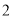 )若
)若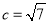 ,且
,且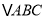 的面积为
的面积为 ,求
,求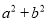 的值.
的值.【答案】(
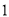 )
)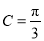 ;(
;(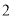 )
)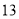
【解析】试题分析:(1)由正弦定理可知,
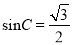 ,所以
,所以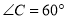 ;(2)由题意,
;(2)由题意, 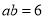 ,
, 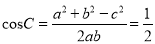 ,得到
,得到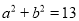 .
.试题解析:
(
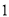 )
)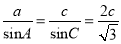 ,∴
,∴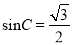 ,
,∵
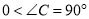 ,∴
,∴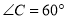 .
.(
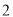 )
)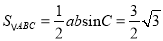 ,
, 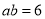 ,
,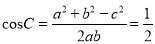 ,
,∴
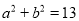 .
.【题型】解答题
【结束】
17【题目】已知等差数列
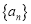 满足:
满足: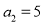 ,
,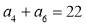 .
.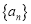 的前n项和为
的前n项和为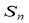 .
.(Ⅰ)求
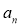 及
及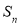 ;
;(Ⅱ)若
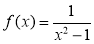 ,
,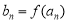 (
(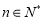 ),求数列
),求数列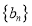 的前
的前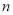 项和
项和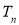 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
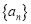 满足:
满足: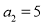 ,
,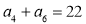 .
.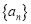 的前n项和为
的前n项和为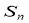 .
.(Ⅰ)求
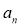 及
及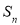 ;
;(Ⅱ)若
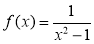 ,
,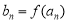 (
(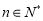 ),求数列
),求数列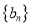 的前
的前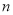 项和
项和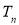 .
.【答案】(Ⅰ)
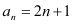 ,
,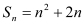 (Ⅱ)
(Ⅱ)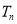 =
=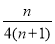
【解析】
试题分析:(Ⅰ)设出首项a1和公差d ,利用等差数列通项公式,就可求出
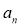 ,再利用等差数列前项求和公式就可求出
,再利用等差数列前项求和公式就可求出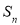 ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知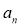 ,再利用
,再利用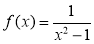 ,
,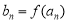 (
(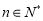 ),就可求出
),就可求出 ,再利用错位相减法就可求出
,再利用错位相减法就可求出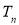 .
.试题解析:(Ⅰ)设等差数列{an}的首项为a1,公差为d
∵
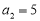 ,
,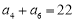 ∴
∴  解得
解得 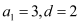
∴
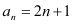
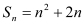 ,
, (Ⅱ)∵
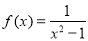 ,
,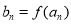 ∴
∴ 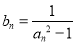
∵
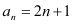 ∴
∴ 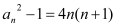
∴
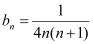
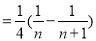
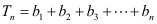
=
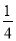 (1-
(1- 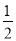 +
+ 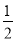 -
- 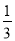 +…+
+…+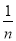 -
-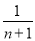 )
) =
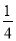 (1-
(1-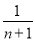 ) =
) =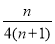
所以数列
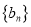 的前
的前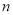 项和
项和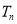 =
=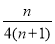 .
.考点:1.等差数列的通项公式; 2. 等差数列的前n项和公式; 3.裂项法求数列的前n项和公式
【题型】解答题
【结束】
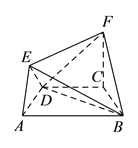
18【题目】在如图所示的几何体中,四边形
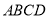 是等腰梯形,
是等腰梯形, 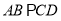 ,
, 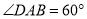 ,
, 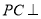 平面
平面 ,
, 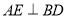 ,
, 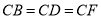 .
.
(
 )求证:
)求证: 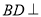 平面
平面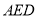 .
.(
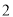 )求二面角
)求二面角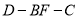 的余弦值.
的余弦值.(
 )在线段
)在线段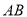 (含端点)上,是否存在一点
(含端点)上,是否存在一点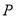 ,使得
,使得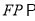 平面
平面 ,若存在,求出
,若存在,求出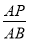 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】港珠澳大桥于2018年10月24日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米,桥面为双向六车道高速公路,大桥通行限速100 km/h. 现对大桥某路段上汽车行驶速度进行抽样调查,画出频率分布直方图(如图).根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过90 km/h的概率分别为

A.
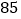 ,
, B.
B.  ,
,
C.
 ,
, D.
D.  ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台为宣传本市,随机对本市内
 岁的人群抽取了
岁的人群抽取了 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y

(1)分别求出
 的值;
的值;(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公司2001年至2017年新产品研发费用
 (单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了
(单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了 与时间变量
与时间变量 的两个线性回归模型.根据2001年至2017年的数据(时间变量
的两个线性回归模型.根据2001年至2017年的数据(时间变量 的值依次为1,2,…,17)建立模型①:
的值依次为1,2,…,17)建立模型①: ;根据2011年至2017年的数据(时间变量
;根据2011年至2017年的数据(时间变量 的值依次为1,2,…,7)建立模型②:
的值依次为1,2,…,7)建立模型②: .
.
(1)分别利用这两个模型,求该公司2019年的新产品研发费用的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
相关试题

