【题目】在锐角△ABC中, ![]() =
= ![]() .
.
(1)求角A;
(2)若a=2,且sinB+cos(C+2B﹣ ![]() )取得最大值时,求△ABC的面积.
)取得最大值时,求△ABC的面积.
参考答案:
【答案】
(1)解:锐角△ABC中,∵ ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() ,∴sinA=
,∴sinA= ![]() ,A=
,A= ![]() .
.
(2)解:由(1)可得B+C= ![]() ,∴C+2B﹣
,∴C+2B﹣ ![]() =B﹣
=B﹣ ![]() ,
,
∴sinB+cos(C+2B﹣ ![]() )=sinB+cos(B﹣
)=sinB+cos(B﹣ ![]() )=
)= ![]() sinB+
sinB+ ![]() cosB=
cosB= ![]() sin(B+
sin(B+ ![]() ),
),
故当B+ ![]() =
= ![]() 时,即B=
时,即B= ![]() 时,sinB+cos(C+2B﹣
时,sinB+cos(C+2B﹣ ![]() )取得最大值
)取得最大值 ![]() ,此时,A=B=C=
,此时,A=B=C= ![]() ,△ABC为等边三角形,
,△ABC为等边三角形,
∴△ABC的面积为 ![]() bcsinA=
bcsinA= ![]() 22
22 ![]() =
= ![]()
【解析】(1)利用余弦定理、诱导公式化简所给的式子,求得sinA 的值,可得A的值.(2)由(1)可得B+C= ![]() ,故有C+2B﹣
,故有C+2B﹣ ![]() =B﹣
=B﹣ ![]() ,再利用两角和差的三角公式、正弦函数的值域求得sinB+cos(C+2B﹣
,再利用两角和差的三角公式、正弦函数的值域求得sinB+cos(C+2B﹣ ![]() )取得最大值
)取得最大值 ![]() ,此时,△ABC为等边三角形,从而求得它的面积.
,此时,△ABC为等边三角形,从而求得它的面积.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
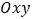 中,已知点
中,已知点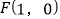 和直线
和直线 :
: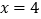 ,圆C与直线
,圆C与直线 相切,并且圆心C关于点
相切,并且圆心C关于点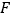 的对称点在圆C上,直线
的对称点在圆C上,直线 与
与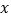 轴相交于点
轴相交于点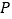 .
.(Ⅰ)求圆心C的轨迹E的方程;
(Ⅱ)过点
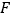 且与直线
且与直线 不垂直的直线
不垂直的直线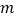 与圆心C的轨迹E相交于点A、B,求
与圆心C的轨迹E相交于点A、B,求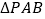 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
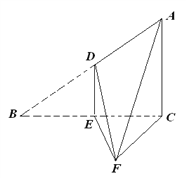
查看答案和解析>>【题目】如图,直角
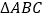 中,∠
中,∠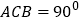 ,
,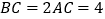 ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将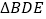 折起至
折起至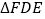 ,且∠
,且∠ .
.(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差为0的等差数列{an}满足a1=1,且a1 , a3﹣2,a9成等比数列.
(1)求数列{an}的通项公式;
(2)记数列{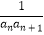 }的前n项和为Sn , 并求使得Sn>
}的前n项和为Sn , 并求使得Sn> 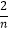 +
+  成立的最小正整数n.
成立的最小正整数n. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖。规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字
 、
、 、
、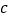 、
、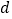 ,摸出来的两个球上的数字之和为该员工所获的奖励额
,摸出来的两个球上的数字之和为该员工所获的奖励额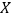 (单位:元)。公司拟定了以下三个数字方案:
(单位:元)。公司拟定了以下三个数字方案:方案


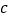
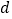
一
100
100
100
500
二
100
100
500
500
三
200
200
400
400
(Ⅰ)如果采取方案一,求
 的概率;
的概率;(Ⅱ)分别计算方案二、方案三的平均数
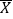 和方差
和方差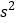 ,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的
 列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?方案二
方案三
合计
男性
12
女性
40
合计
82
100
附:
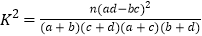
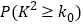
0.15
0.10
0.05
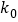
2.072
2.706
3.841
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
极坐标系的极点在平面直角坐标系的原点
 处,极轴与
处,极轴与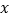 轴的正半轴重合,两坐标系单位长度相同.已知曲线
轴的正半轴重合,两坐标系单位长度相同.已知曲线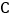 的极坐标方程为
的极坐标方程为 ,直线
,直线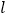 的参数方程为
的参数方程为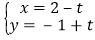 (
(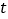 为参数)。
为参数)。(Ⅰ)将直线
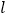 的参数方程化为普通方程,曲线
的参数方程化为普通方程,曲线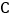 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(Ⅱ)设曲线
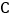 上到直线
上到直线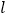 的距离为
的距离为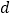 的点的个数为
的点的个数为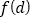 ,求
,求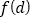 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线E:x2=2py(p>0),直线y=kx+2与E交于A、B两点,且

 =2,其中O为原点.
=2,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为(0,﹣2),记直线CA、CB的斜率分别为k1 , k2 , 证明:k12+k22﹣2k2为定值.
相关试题

