【题目】已知f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围.
参考答案:
【答案】(1)当a≤0时,f(x)的单调增区间为(-∞,+∞);当a>0时,f(x)的单调增区间为(lna,+∞).(2)(-∞,0].
【解析】试题分析:(1)![]() ,根据其导函数
,根据其导函数![]() 的解即
的解即![]() 的情况讨论
的情况讨论![]() 的符号,即得其单调区间;(2)若
的符号,即得其单调区间;(2)若![]() 在定义域
在定义域![]() 内单调递增,则
内单调递增,则![]() 恒成立,所以
恒成立,所以![]() 恒成立,即
恒成立,即![]() 即得
即得![]() 的取值范围.
的取值范围.
试题解析:(1)∵f(x)=ex-ax-1(x∈R),∴f′(x)=ex-a.令f′(x)≥0,得ex≥a.当a≤0时,f′(x)>0在R上恒成立;当a>0时,有x≥ln a.综上,当a≤0时,f(x)的单调增区间为(-∞,+∞);当a>0时,f(x)的单调增区间为(ln a,+∞).
(2)由(1)知f′(x)=ex-a.∵f(x)在R上单调递增,
∴f′(x)=ex-a≥0恒成立,即a≤ex在R上恒成立.
∵x∈R时,ex>0,∴a≤0,
即a的取值范围是(-∞,0].
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知p:方程
 有两个不等的负实根,q:方程
有两个不等的负实根,q:方程 无实根,若
无实根,若 为真,
为真, 为假,求实数m的取值范围。
为假,求实数m的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,
,  .
.(1)若
 是
是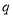 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围;
的取值范围;(2)若
 ,“
,“ ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
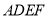 与梯形
与梯形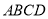 所在的平面相互垂直,
所在的平面相互垂直, 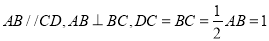 ,点
,点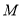 在线段
在线段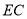 上.
上.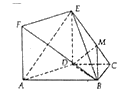
(1)证明:平面
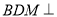 平面
平面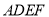 ;
;(2)若
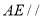 平面
平面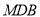 ,求三棱锥
,求三棱锥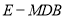 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一名同学家开了一个小卖部,他为了研究气温对某种引领销售的影响,记录了2015年7月至12月每月15号下午14时的气温和当天的饮料杯数,得到如下资料:

该同学确定的研究方案是:现从这六组数据中选取2组,用剩下的4组数据取线性回归方程,再用被选中的2组数据进行检验.
(1)求选取2组数据恰好是相邻两个月的概率;
(2)若选中的是8月与12月的两组数据,根据剩下的4组数据,求出
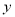 关于
关于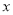 的线性回归方程
的线性回归方程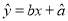 ;
;(3)若有线性回归方程得到估计,数据与所宣称的检验数据的误差不超过3杯,则认为得到的线性回归方程是理想的,请问(2)所得线性回归方程是否理想.
附:对于一组数据
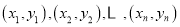 ,其回归直线
,其回归直线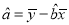 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 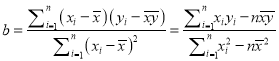 ,
, 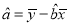 ,
, 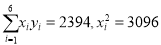 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市在元旦期间开展优惠酬宾活动,凡购物满100元可抽奖一次,满200元可抽奖两次…依此类推.抽奖箱中有7个白球和3个红球,其中3个红球上分别标有10元,10元,20元字样.每次抽奖要从抽奖箱中有放回地任摸一个球,若摸到红球,根据球上标注金额奖励现金;若摸到白球,没有任何奖励.
(Ⅰ)一次抽奖中,已知摸中了红球,求获得20元奖励的概率;
(Ⅱ)小明有两次抽奖机会,用
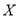 表示他两次抽奖获得的现金总额,写出
表示他两次抽奖获得的现金总额,写出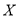 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,多面体
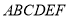 中,
中, 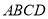 是正方形,
是正方形, 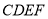 是梯形,
是梯形, 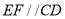 ,
, 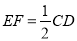 ,
, 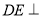 平面
平面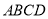 且
且 ,
, 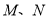 分别为棱
分别为棱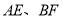 的中点.
的中点.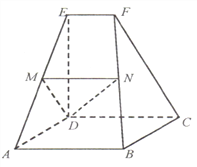
(Ⅰ)求证:平面
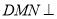 平面
平面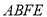 ;
;(Ⅱ)求平面
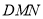 和平面
和平面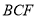 所成锐二面角的余弦值.
所成锐二面角的余弦值.
相关试题

