【题目】已知命题P:函数![]() 是增函数,命题Q:
是增函数,命题Q:![]()
(1)写出命题Q的否命题![]() ,并求出实数
,并求出实数![]() 的取值范围,使得命题
的取值范围,使得命题![]() 为真命题;
为真命题;
(2)如果![]() 是真命题,
是真命题,![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)否命题![]() ,就是把命题
,就是把命题![]() 的条件和结论都否定,联系对应二次函数图象,由
的条件和结论都否定,联系对应二次函数图象,由![]() ,解得
,解得![]() 的取值范围;(2)命题
的取值范围;(2)命题![]() 和命题
和命题![]() 中,一个真命题,一个为假命题,分命题
中,一个真命题,一个为假命题,分命题![]() 真命题且
真命题且![]() 是假命题、命题
是假命题、命题![]() 是假命题且
是假命题且![]() 是真命题,两种情况,计算可得答案.
是真命题,两种情况,计算可得答案.
试题解析:(1)![]() :
:![]() ,
,![]()
若![]() 为真命题,则
为真命题,则![]() 解得:
解得:![]() 或
或![]()
故所求实数![]() 的取值范围为:
的取值范围为:![]()
(2)若函数![]() 是增函数,则
是增函数,则![]()
又![]()
![]() 为真命题时,由
为真命题时,由![]()
![]() 的取值范围为
的取值范围为![]()
由“![]() ” 为真命题,“
” 为真命题,“![]() ”为假命题,故命题
”为假命题,故命题![]() 、
、![]() 中有且仅有一个真命题
中有且仅有一个真命题
当![]() 真
真![]() 假时,实数
假时,实数![]() 的取值范围为:
的取值范围为:![]()
当![]() 假
假![]() 真时,实数
真时,实数![]() 的取值范围为:
的取值范围为:![]()
综上可知实数![]() 的取值范围:
的取值范围:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,平面
中,平面 平面
平面 ,底面
,底面 为梯
为梯形,
 ,
,  ,
,  .且
.且 与
与 均为正三角形,
均为正三角形,  为
为 的中点,
的中点, 为
为 重心.
重心.
(1)求证:
 平面
平面 ;
;(2)求异面直线
 与
与 的夹角的余弦值.
的夹角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知椭圆
 :
: 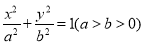 的左,右焦点分别为
的左,右焦点分别为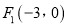 ,
, 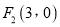 .点
.点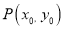 是椭圆
是椭圆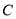 在
在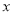 轴上方的动点,且△
轴上方的动点,且△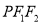 的周长为16.
的周长为16. 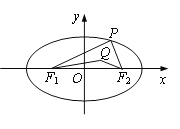
(1)求椭圆
 的方程;
的方程;(2)设点
 到△
到△ 三边的距离均相等.
三边的距离均相等.①当
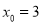 时,求点
时,求点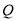 的坐标;
的坐标;②求证:点
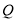 在定椭圆上.
在定椭圆上. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
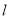 的参数方程为
的参数方程为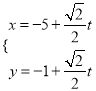 (其中
(其中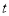 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, 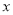 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线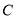 的极坐标方程为
的极坐标方程为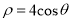 .
.(1)写出直线
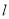 和曲线
和曲线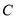 的普通方程;
的普通方程;(2)已知点
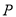 为曲线
为曲线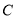 上的动点,求
上的动点,求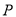 到直线
到直线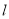 的距离的最大值.
的距离的最大值. -
科目: 来源: 题型:
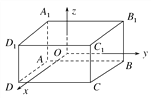
查看答案和解析>>【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为常数.
为常数. (1)判断函数
 的单调性并证明;
的单调性并证明;(2)当
 时,对于任意
时,对于任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正四棱锥P-ABCD中,底面边长为2,侧棱长为
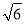 ,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.
,M,N分别为AB,BC的中点,以O为原点,射线OM,ON,OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系.若E,F分别为PA,PB的中点,求A,B,C,D,E,F的坐标.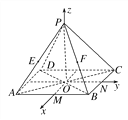
相关试题

