【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为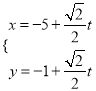 (其中
(其中![]() 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
参考答案:
【答案】(1)直线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)消去参数![]() ,即可得到直线
,即可得到直线![]() 的普通方程,利用
的普通方程,利用![]() ,
, ![]() ,即可得到曲线
,即可得到曲线![]() 的普通方程;(2)利用几何性质,点到直线的距离的最大值为圆心到直线的距离与圆的半径之和,即可求解.
的普通方程;(2)利用几何性质,点到直线的距离的最大值为圆心到直线的距离与圆的半径之和,即可求解.
试题解析:(1)由题意,消去直线![]() 的参数方程中的参数
的参数方程中的参数![]() ,得普通方程为
,得普通方程为![]() ,
,
又由![]() ,得
,得![]() ,由
,由![]() 得曲线
得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)曲线![]()
![]() 可化为
可化为![]() ,圆心
,圆心![]() 到直线的距离为
到直线的距离为![]() ,再加上半径
,再加上半径![]() ,即为
,即为![]() 到直线
到直线![]() 距离的最大值
距离的最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵
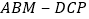 与刍童
与刍童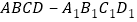 的组合体中
的组合体中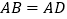 ,
,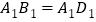 .台体体积公式:
.台体体积公式: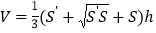 ,其中
,其中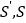 分别为台体上、下底面面积,
分别为台体上、下底面面积,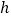 为台体高.
为台体高.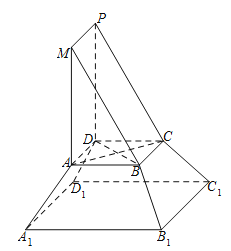
(Ⅰ)证明:直线
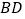
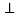 平面
平面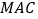 ;
;(Ⅱ)若
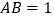 ,
,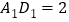 ,
,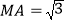 ,三棱锥
,三棱锥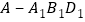 的体积
的体积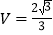 ,求该组合体的体积.
,求该组合体的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,平面
中,平面 平面
平面 ,底面
,底面 为梯
为梯形,
 ,
,  ,
,  .且
.且 与
与 均为正三角形,
均为正三角形,  为
为 的中点,
的中点, 为
为 重心.
重心.
(1)求证:
 平面
平面 ;
;(2)求异面直线
 与
与 的夹角的余弦值.
的夹角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知椭圆
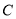 :
: 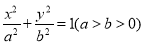 的左,右焦点分别为
的左,右焦点分别为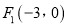 ,
, 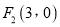 .点
.点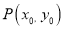 是椭圆
是椭圆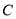 在
在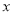 轴上方的动点,且△
轴上方的动点,且△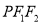 的周长为16.
的周长为16. 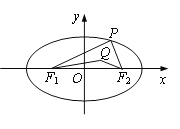
(1)求椭圆
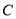 的方程;
的方程;(2)设点
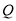 到△
到△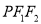 三边的距离均相等.
三边的距离均相等.①当
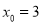 时,求点
时,求点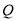 的坐标;
的坐标;②求证:点
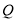 在定椭圆上.
在定椭圆上. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题P:函数
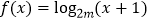 是增函数,命题Q:
是增函数,命题Q: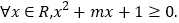
(1)写出命题Q的否命题
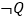 ,并求出实数
,并求出实数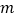 的取值范围,使得命题
的取值范围,使得命题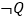 为真命题;
为真命题;(2)如果
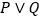 是真命题,
是真命题,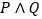 是假命题,求实数
是假命题,求实数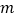 的取值范围.
的取值范围. -
科目: 来源: 题型:
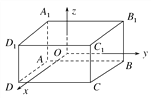
查看答案和解析>>【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为常数.
为常数. (1)判断函数
 的单调性并证明;
的单调性并证明;(2)当
 时,对于任意
时,对于任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
相关试题

