【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),离心率e=
=1(a>b>0),离心率e= ![]() ,已知点P(0,
,已知点P(0, ![]() )到椭圆C的右焦点F的距离是
)到椭圆C的右焦点F的距离是 ![]() .设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
.设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)求点Q的横坐标x0的取值范围.
参考答案:
【答案】解:(Ⅰ)由题意可得:e= ![]() =
= ![]() ,
, ![]() =
= ![]() ,又a2+b2=c2 . 联立解得:c2=12,a=4,b=2.
,又a2+b2=c2 . 联立解得:c2=12,a=4,b=2.
∴椭圆C的标准方程为: ![]() =1.
=1.
(Ⅱ)设直线AB的方程为:y=kx+ ![]() ,(k≠0),A(x1 , y1),B(x2 , y2),线段AB的中点M(x3 , y3),线段AB的中垂线方程为:y﹣y3=﹣
,(k≠0),A(x1 , y1),B(x2 , y2),线段AB的中点M(x3 , y3),线段AB的中垂线方程为:y﹣y3=﹣ ![]() (x﹣x3).
(x﹣x3).
联立  ,化为:(1+4k2)x2+12kx﹣7=0,
,化为:(1+4k2)x2+12kx﹣7=0,
△>0,∴x1+x2=﹣ ![]() ,
,
∴x3= ![]() =﹣
=﹣ ![]() .
.
y3=kx3+ ![]() =
= ![]() .
.
∴线段AB的中垂线方程为:y﹣ ![]() =﹣
=﹣ ![]() (x+
(x+ ![]() ).
).
令y=0,可得x0= ![]() =
=  ,
,
k>0时,0>x0≥ ![]() .
.
k<0时,0<x0≤ ![]() .
.
k=0时,x0=0也满足条件.
综上可得:点Q的横坐标x0的取值范围是 ![]()
【解析】(Ⅰ)由题意可得:e= ![]() =
= ![]() ,
, ![]() =
= ![]() ,又a2+b2=c2 . 联立解出即可得出.(Ⅱ)设直线AB的方程为:y=kx+
,又a2+b2=c2 . 联立解出即可得出.(Ⅱ)设直线AB的方程为:y=kx+ ![]() ,(k≠0),A(x1 , y1),B(x2 , y2),线段AB的中点M(x3 , y3),直线AB的方程与题意方程联立化为:(1+4k2)x2+12kx﹣7=0,利用中点坐标公式与根与系数的关系可得可得中点M的坐标,可得线段AB的中垂线方程,令y=0,可得x0 , 通过对k分类讨论,利用基本不等式的性质即可得出.
,(k≠0),A(x1 , y1),B(x2 , y2),线段AB的中点M(x3 , y3),直线AB的方程与题意方程联立化为:(1+4k2)x2+12kx﹣7=0,利用中点坐标公式与根与系数的关系可得可得中点M的坐标,可得线段AB的中垂线方程,令y=0,可得x0 , 通过对k分类讨论,利用基本不等式的性质即可得出.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆
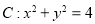 与
与 轴的左右交点分别为
轴的左右交点分别为 ,与
,与 轴正半轴的交点为
轴正半轴的交点为 .
.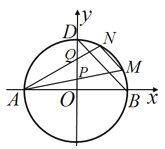
(1)若直线
 过点
过点 并且与圆
并且与圆 相切,求直线
相切,求直线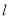 的方程;
的方程;(2)若点
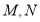 是圆
是圆 上第一象限内的点,直线
上第一象限内的点,直线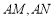 分别与
分别与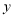 轴交于点
轴交于点 ,点
,点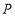 是线段
是线段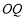 的中点,直线
的中点,直线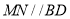 ,求直线
,求直线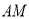 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面凸四边形
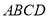 中(凸四边形指没有角度数大于
中(凸四边形指没有角度数大于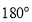 的四边形),
的四边形),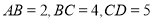 .
.
(1)若
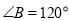 ,
,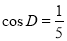 ,求
,求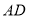 ;
;(2)已知
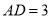 ,记四边形
,记四边形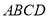 的面积为
的面积为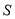 .
.① 求
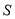 的最大值;
的最大值;② 若对于常数
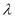 ,不等式
,不等式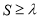 恒成立,求实数
恒成立,求实数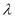 的取值范围.(直接写结果,不需要过程)
的取值范围.(直接写结果,不需要过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
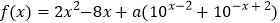 有唯一零点,则a=
有唯一零点,则a=A.
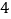 B.
B. 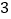 C.
C. 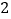 D.
D. 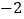
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若
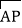 =
=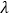
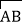 +
+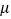
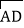 ,则
,则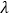 +
+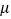 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车
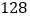 辆,混合动力型公交车
辆,混合动力型公交车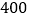 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加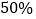 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入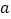 辆.设
辆.设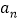 、
、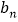 分别为第
分别为第 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设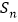 、
、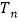 分别为
分别为 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。(1)求
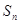 、
、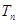 ,并求
,并求 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数 ;
;(2)该市计划用
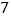 年的时间完成全部更换,求
年的时间完成全部更换,求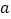 的最小值.
的最小值.
相关试题

