【题目】已知函数![]() 有唯一零点,则a=
有唯一零点,则a=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】分析:通过转化可知问题等价于函数y=1﹣(x﹣1)2的图象与y=a(![]() +
+![]() )的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.
)的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.
详解:因为f(x)![]() =﹣8+2(x﹣2)2+a(
=﹣8+2(x﹣2)2+a(![]() +
+![]() )=0,
)=0,
所以函数f(x)有唯一零点等价于方程8﹣2(x﹣2)2= a(![]() +
+![]() )有唯一解,
)有唯一解,
等价于函数y=8﹣2(x﹣2)2的图象与y= a(![]() +
+![]() )的图象只有一个交点.
)的图象只有一个交点.
当a=0时,f(x)=![]() ≥﹣8,此时有两个零点,矛盾;
≥﹣8,此时有两个零点,矛盾;
当a<0时,由于y=8﹣2(x﹣2)2在(﹣∞,2)上递增、在(2,+∞)上递减,
且a(![]() +
+![]() )在(﹣∞,2)上递增、在(2,+∞)上递减,
)在(﹣∞,2)上递增、在(2,+∞)上递减,
所以函数y=8﹣2(x﹣2)2的图象的最高点为A(2,8),y= a(![]() +
+![]() )的图象的最高点为B(2,2a),
)的图象的最高点为B(2,2a),
由于2a<0<8,此时函数y=8﹣2(x﹣2)2的图象与a(![]() +
+![]() )的图象有两个交点,矛盾;
)的图象有两个交点,矛盾;
当a>0时,由于y=8﹣2(x﹣2)2在(﹣∞,2)上递增、在(2,+∞)上递减,
且y= a(![]() +
+![]() )在(﹣∞,2)上递减、在(2,+∞)上递增,
)在(﹣∞,2)上递减、在(2,+∞)上递增,
所以函数y=8﹣2(x﹣2)2的图象的最高点为A(2,8),y= a(![]() +
+![]() )的图象的最低点为B(2,2a),
)的图象的最低点为B(2,2a),
由题可知点A与点B重合时满足条件,即2a=8,即a=![]() ,符合条件;
,符合条件;
综上所述,a=![]() ,
,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面凸四边形
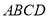 中(凸四边形指没有角度数大于
中(凸四边形指没有角度数大于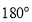 的四边形),
的四边形),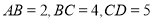 .
.
(1)若
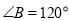 ,
,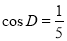 ,求
,求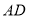 ;
;(2)已知
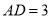 ,记四边形
,记四边形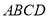 的面积为
的面积为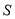 .
.① 求
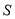 的最大值;
的最大值;② 若对于常数
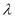 ,不等式
,不等式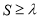 恒成立,求实数
恒成立,求实数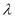 的取值范围.(直接写结果,不需要过程)
的取值范围.(直接写结果,不需要过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 +
+  =1(a>b>0),离心率e=
=1(a>b>0),离心率e=  ,已知点P(0,
,已知点P(0,  )到椭圆C的右焦点F的距离是
)到椭圆C的右焦点F的距离是  .设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
.设经过点P且斜率存在的直线与椭圆C相交于A、B两点,线段AB的中垂线与x轴相交于一点Q. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)求点Q的横坐标x0的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若
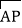 =
=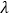
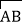 +
+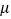
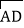 ,则
,则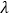 +
+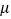 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车
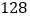 辆,混合动力型公交车
辆,混合动力型公交车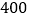 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加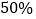 ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入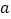 辆.设
辆.设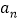 、
、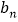 分别为第
分别为第 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设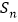 、
、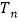 分别为
分别为 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。(1)求
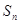 、
、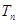 ,并求
,并求 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数 ;
;(2)该市计划用
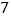 年的时间完成全部更换,求
年的时间完成全部更换,求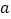 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
相关试题

