【题目】为了解防震知识在中学生中的普及情况,某地震部门命制了一份满分为10分的问卷到红星中学做问卷调查.该校甲、乙两个班各被随机抽取![]() 名学生接受问卷调查,甲班
名学生接受问卷调查,甲班![]() 名学生得分为5,8,9,9,9乙班5名学生得分为6,7,8,9,10.
名学生得分为5,8,9,9,9乙班5名学生得分为6,7,8,9,10.
(Ⅰ)请你估计甲乙两个班中,哪个班的问卷得分更稳定一些;
(Ⅱ)如果把乙班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率.
参考答案:
【答案】(1);(2).
【解析】试题分析:(Ⅰ)计算分别可得平均分和方差,可得结论;
(Ⅱ)列举可得总的基本事件共10个,符合题意的共4个,由概率公式可得.
试题解析:
(Ⅰ)因为甲班的![]() 名学生的平均得分为
名学生的平均得分为![]() ÷
÷![]() ,
,
所以方差![]() ;
;
又乙班![]() 名学生的平均得分为
名学生的平均得分为![]() ÷
÷![]() ,
,
所以方差![]() .
.
所以![]() ,
,
因此,乙班的问卷调查得分更稳定一些.
(Ⅱ)从乙班![]() 名同学的得分中任选
名同学的得分中任选![]() 个的基本事件空间
个的基本事件空间![]() =
=![]() ,
,
![]() 共10个基本事件,
共10个基本事件,
设事件![]() 为“样本平均数与总体平均数之差的绝对值不小于
为“样本平均数与总体平均数之差的绝对值不小于![]() ”,则
”,则
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
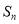 为数列
为数列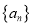 的前
的前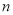 项和,对任意的
项和,对任意的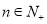 ,都有
,都有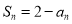 ,数列
,数列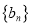 满足
满足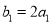 ,
, 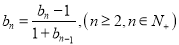 .
.(1)求证:数列
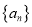 是等比数列,并求
是等比数列,并求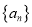 的通项公式;
的通项公式;(2)求数列
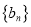 的通项公式;
的通项公式;(3)求数列
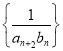 的前
的前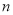 项和
项和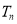 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足
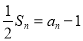 ,
,(1)求数列{an}的通项公式;
(2)求证:数列{an}中的任意三项不可能成等差数列;
(3)设
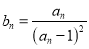 ,Tn为{bn}的前n项和,求证
,Tn为{bn}的前n项和,求证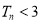 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
-
科目: 来源: 题型:
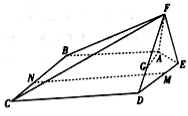
查看答案和解析>>【题目】如图,在五棱锥
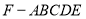 中,平面
中,平面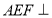 平面
平面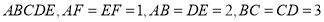 ,且
,且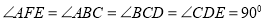 .
.
(1)已知点
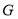 在线段
在线段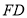 上,确定
上,确定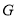 的位置,使得
的位置,使得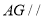 平面
平面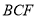 ;
;(2)点
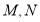 分别在线段
分别在线段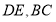 上,若沿直线
上,若沿直线 将四边形
将四边形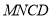 向上翻折,
向上翻折,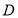 与
与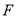 恰好重合,求三棱锥
恰好重合,求三棱锥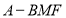 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
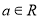 ,函数
,函数 .
.(1)求证:曲线
 在点
在点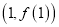 处的切线过定点;
处的切线过定点;(2)若
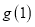 是
是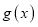 在区间
在区间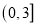 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数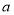 的取值范围;
的取值范围;(3)求证:对任意给定的正数
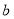 ,总存在
,总存在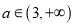 ,使得
,使得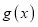 在
在 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中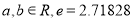 是自然对数的底数.
是自然对数的底数.(1)若曲线
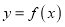 在
在 处的切线方程为
处的切线方程为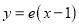 .求实数
.求实数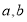 的值;
的值;(2)①若
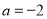 时,函数
时,函数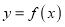 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数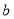 的取值范围;
的取值范围;②若
 ,若
,若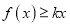 对一切正实数
对一切正实数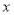 恒成立,求实数
恒成立,求实数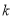 的取值范围(用
的取值范围(用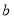 表示).
表示).
相关试题

