【题目】已知函数(x)=xlnx,g(x)=ax3-![]() .
.
(Ⅰ)求函数(x)的单调递增区间和最小值;
(Ⅱ)若函数y= (x)与函数y =g(x)的图象在交点处存在公共切线,求实数a的值。
参考答案:
【答案】(Ⅰ) 见解析;(Ⅱ)a=![]() .
.
【解析】试题分析:(Ⅰ)求出![]() 的导数,求得单调区间和极值,即可得最小值;(Ⅱ)设函数
的导数,求得单调区间和极值,即可得最小值;(Ⅱ)设函数![]() 与函数
与函数![]() 的图象在交点
的图象在交点![]() 处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得
处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得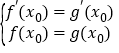 ,列出方程组,结合(Ⅰ),即可求出实数
,列出方程组,结合(Ⅰ),即可求出实数![]() 的值.
的值.
试题解析:(Ⅰ)∵![]()
∴![]() ,
,![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴所求函数![]() 的单调递增区间为
的单调递增区间为![]() ,最小值为
,最小值为![]() .
.
(Ⅱ) 设函数![]() 与函数
与函数![]() 的图象在交点
的图象在交点![]() 处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得
处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得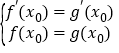 , 即
, 即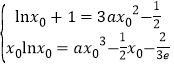 (*),变形得
(*),变形得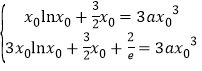 .
.
∴![]() ,化简得
,化简得![]()
∴![]() 是方程
是方程![]() 的一个实数解.
的一个实数解.
又∵由(Ⅰ)易知方程![]() 有唯一的实数解,且该解为
有唯一的实数解,且该解为![]()
∴![]() ,将之代入
,将之代入![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为[﹣1,1],图象如图1所示;函数g(x)的定义域为[﹣2,2],图象如图2所示,设函数f(g(x))有m个零点,函数g(f(x))有n个零点,则m+n等于( )
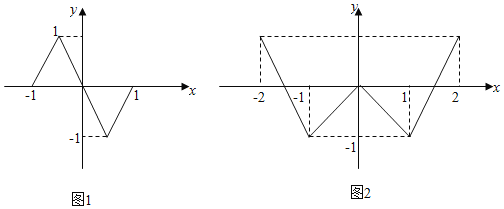
A. 6 B. 10 C. 8 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年9月3日,抗战胜利71周年纪念活动在北京隆重举行,受到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、拥待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这个环节(可参加多个,也可都不参加)的情况及其概率如下表所示:

(Ⅰ)若m=2n,则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈,求从参加纪念活动环节数为1的抗战老兵中抽取的人数;
(Ⅱ)某医疗部门决定从(Ⅰ)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】十八届五中全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策。提高生殖健康、妇幼保健、托幼等公共服务水平。为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了200位30到40岁的公务员,得到情况如下表:

(Ⅰ)是否有99%以上的把握认为“生二胎与性别有关”,并说明理由;
(Ⅱ)将频率看作概率,现从社会上随机抽取甲、乙、丙3位30到40 岁的男公务员,求这三人中至少有一人要生二胎的概率.
附:
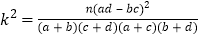

-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy 中,曲线C的参数方程为
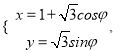 (
(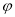 是参数,0≤
是参数,0≤ ≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)直线l1,的极坐标方程是2psin(θ+
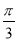 )+
)+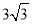 =0,直线l2:θ =
=0,直线l2:θ =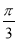 与曲线C的交点为P,与直线l1的交点为Q,求线段PQ的长.
与曲线C的交点为P,与直线l1的交点为Q,求线段PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—5:不等式选讲
已知函数(x)=|2x-a|+ |x -1|.
(Ⅰ)当a=3时,求不等式(x)≥2的解集;
(Ⅱ)若(x)≥5-x对
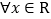 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是( )
A. 至少有一个白球;至少有一个红球 B. 至少有一个白球;红、黑球各一个
C. 恰有一个白球;一个白球一个黑球 D. 至少有一个白球;都是白球
相关试题

