【题目】当![]() ,则称点
,则称点![]() 为平面上单调格点:设
为平面上单调格点:设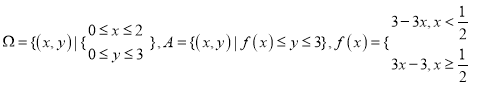
求从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上的概率;
上的概率;
求从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点的概率.
上的格点的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)作出集合![]() 所对应的区域,记事件
所对应的区域,记事件![]() “从区域
“从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上”,根据几何概型,利用面积比,即可求解概率;
上”,根据几何概型,利用面积比,即可求解概率;
(2)事件![]() “从区域
“从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点”,得出基本事件的总数,和事件
上的格点”,得出基本事件的总数,和事件![]() 所包含的基本事件的个数,利用古典概型及概率的计算公式,即可求解事件的概率.
所包含的基本事件的个数,利用古典概型及概率的计算公式,即可求解事件的概率.
试题解析:
作出集合![]() 所对应的区域(如图):
所对应的区域(如图):
矩形![]()
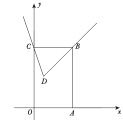
则:(1)记事件![]() “从区域
“从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上”
上”
则事件![]() 符合几何概型,即
符合几何概型,即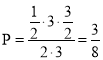 .
.
(2)事件![]() “从区域
“从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点”
上的格点”
则事件![]() 符合古典概型,区域
符合古典概型,区域![]() 中的格点个数:当横坐标分别为0,1,2时,纵坐标可以为0,1,2,3中的任一个,此时有
中的格点个数:当横坐标分别为0,1,2时,纵坐标可以为0,1,2,3中的任一个,此时有![]() 个;而区域
个;而区域![]() 上的格点有(0,3),(1,2),(2,3),(1,2)共4个,
上的格点有(0,3),(1,2),(2,3),(1,2)共4个,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
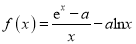 ,其中
,其中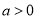 ,
, 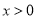 ,
, 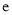 是自然对数的底数.
是自然对数的底数.(Ⅰ)讨论
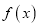 的单调性;
的单调性;(Ⅱ)设函数
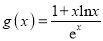 ,证明:
,证明: 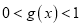 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的二次项系数为a,且不等式f(x)+2x>0的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的前n项和Sn , 首项a1=a,公比为q(q≠0且q≠1).
(1)推导证明:Sn=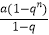 ;
;
(2)等比数列{an}中,是否存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列?若存在,求出符合条件的等比数列公比q的值,若不存在,说明理由;
(3)本题中,若a=q=2,已知数列{nan}的前n项和Tn , 是否存在正整数n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积
 ;
;(2)求该几何体的表面积
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为
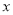 (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )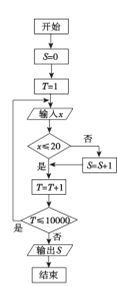
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
相关试题

