【题目】已知等比数列{an}的前n项和Sn , 首项a1=a,公比为q(q≠0且q≠1).
(1)推导证明:Sn= ![]() ;
;
(2)等比数列{an}中,是否存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列?若存在,求出符合条件的等比数列公比q的值,若不存在,说明理由;
(3)本题中,若a=q=2,已知数列{nan}的前n项和Tn , 是否存在正整数n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵Sn=a1+a2+a3+…+an=a1+a1q+a1q2+…+a1qn﹣1,①
∴qSn=a1q+a1q2+a1q3+…+a1qn,②
①﹣②可得(1﹣q)Sn=a1﹣a1qn,
当q≠1时,上式两边同除以1﹣q可得Sn= ![]()
(2)解:不存在存在连续的三项:ak、ak+1、ak+2,使得这三项成等差数列.
证明如下:若ak、ak+1、ak+2成等差数列,则: ![]()
∵ak≠0∴q2﹣q+1=0
而 ![]()
∴不存在存在连续的三项:ak、ak+1、ak+2,使得这三项成等差数列
(3)解:Tn=1×21+2×22+…+n×2n①
2Tn=1×22+2×23+3×24+…+n×2n+1 ②
① ﹣②得Tn=n×2n+1﹣(21+22+23+…+2n)=(n﹣1)2n+1+2
由于Tn是递增的,当n=7时 ![]() ;
;
当n=8时 ![]() .
.
所以存在正整数n,使得Tn≥2016的取值集合为{n|n≥8,n∈N+}
【解析】(1)利用错位相减法真假求解即可.(2)不存在存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列.利用等差数列的等差中项列出关系式,推出矛盾结果.(3)利用错位相减法求出前n项和,通过数列的单调性判断n=7与8时,推出结果即可.
【考点精析】掌握等比数列的基本性质是解答本题的根本,需要知道{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的二次项系数为a,且不等式f(x)+2x>0的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】当
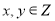 ,则称点
,则称点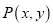 为平面上单调格点:设
为平面上单调格点:设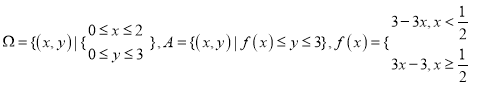
求从区域
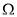 中任取一点
中任取一点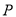 ,而该点落在区域
,而该点落在区域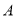 上的概率;
上的概率;求从区域
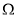 中的所有格点中任取一点
中的所有格点中任取一点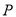 ,而该点是区域
,而该点是区域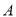 上的格点的概率.
上的格点的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积
 ;
;(2)求该几何体的表面积
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某机构为调查2017年下半年落实中学生“阳光体育”活动的情况,设平均每人每天参加体育锻炼时间为
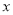 (单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )
(单位:分钟),按锻炼时间分下列四种情况统计:①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上,有10000名中学生参加了此项活动,图1是此次调查中某一项的流程图,其输出的结果是6400,则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是( )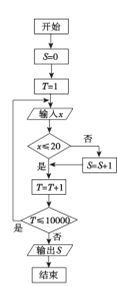
图1
A. 0.64 B. 0.36 C. 6400 D. 3600
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
相关试题

