搜索
【题目】有下列说法： ①线性回归分析就是由样本点去寻找一条直线，使之贴近这些样本点的数学方法；②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归方程 
，可以估计和观测变量的取值和变化趋势；④因为由任何一组观测值都可以求得一个线性回归方程，所以没有必要进行相关性检验.其中正确命题的个数是（ ）
A.1
B.2
C.3
D.4
参考答案：
【答案】C
【解析】解答：①反映的正是最小二乘法思想，故正确.②反映的是散点图的作用，也正确.③解释的是回归方程 
的作用，故也正确.④是不正确的，在求回归方程之前必须进行相关性检验，以体现两变量的关系. 分析：本题主要考查了回归分析，解决问题的关键是回归分析的过程；（1）随机抽取样本，确定数据，形成样本点；（2）由样本点形成散点图，判断是否具有线性相关关系；（3）由最小二乘法确定线性回归方程；（4）由回归方程观察变量的取值及变化趋势
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知O、A、B三地在同一水平面内，A地在O地正东方向2km处，B地在O地正北方向2km处，某测绘队员在A、B之间的直线公路上任选一点C作为测绘点，用测绘仪进行测绘，O地为一磁场，距离其不超过
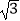km的范围内会测绘仪等电子仪器形成干扰，使测量结果不准确，则该测绘队员能够得到准确数据的概率是（ ）
A.1-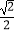
B.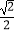
C.1-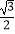
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知全集U={x|x2﹣3x+2≥0}，A={x||x﹣2|＞1}，B=
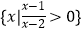
求：
（1）A∩B；
（2）A∩UB；
（3）U（A∪B）． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=log2（x+1），g（x）=log2（3x+1）．
（1）求出使g（x）≥f（x）成立的x的取值范围；
（2）在（1）的范围内求y=g（x）﹣f（x）的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】经市场调查：生产某产品需投入年固定成本为3万元，每生产x万件，需另投入流动成本为W（x）万元，在年产量不足8万件时，W（x）=
x2+x（万元），在年产量不小于8万件时，W（x）=6x+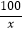 
﹣38（万元）．通过市场分析，每件产品售价为5元时，生产的商品能当年全部售完．
（1）写出年利润L（x）（万元）关于年产量x（万件）的函数解析式；
（2）写出当产量为多少时利润最大，并求出最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=ax2+bx+1（a，b为实数），x∈R，
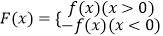
（1）若f（﹣1）=0，且函数f（x）的值域为[0，+∞），求F（x）的表达式；
（2）在（1）的条件下，当x∈[﹣2，2]时，g（x）=f（x）﹣kx是单调函数，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0且f（x）为偶函数，判断F（m）+F（n）能否大于零． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知定点A（0，1），B（0，﹣1），C（1，0），动点P满足：
，（1）求动点P的轨迹方程，并说明方程表示的曲线类型；
（2）当k=2，求
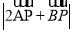的取值范围。
相关试题
