搜索
【题目】已知定点A（0，1），B（0，﹣1），C（1，0），动点P满足： 
，
（1）求动点P的轨迹方程，并说明方程表示的曲线类型；
（2）当k=2，求
的取值范围。
参考答案：
【答案】（1）见解析（2）
【解析】试题分析：（1）设P（x，y）代入向量数量积坐标运算，求得轨迹方程。（2）由（1）得x2+y2=4x﹣3，把所求向量模坐标化
转化为求t=6x﹣y的范围，其中x,y满足x2+y2=4x﹣3，转化为直线与圆相交。
试题解析：（1）设P（x，y），
．
当k=1时，由
，得x2+y2﹣1=（1﹣x）2+y2，
整理得：x=1，表示过（1，0）且平行于y轴的直线；
当k≠1时，由
，得x2+y2﹣1=k（1﹣x）2+ky2，
整理得： 
，表示以点
为圆心，以
为半径的圆．
（2）当k=2时，方程化为（x﹣2）2+y2=1，即x2+y2=4x﹣3，
∵
∴
，又x2+y2=4x﹣3，
∴
．问题归结为求6x﹣y的最值，
令t=6x﹣y，
∵点P在圆（x﹣2）2+y2=1，圆心到直线t=6x﹣y的距离不大于圆的半径，
∴
，解得
．∴
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有下列说法： ①线性回归分析就是由样本点去寻找一条直线，使之贴近这些样本点的数学方法；②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归方程
，可以估计和观测变量的取值和变化趋势；④因为由任何一组观测值都可以求得一个线性回归方程，所以没有必要进行相关性检验.其中正确命题的个数是（ ）
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】经市场调查：生产某产品需投入年固定成本为3万元，每生产x万件，需另投入流动成本为W（x）万元，在年产量不足8万件时，W（x）=
x2+x（万元），在年产量不小于8万件时，W（x）=6x+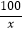 
﹣38（万元）．通过市场分析，每件产品售价为5元时，生产的商品能当年全部售完．
（1）写出年利润L（x）（万元）关于年产量x（万件）的函数解析式；
（2）写出当产量为多少时利润最大，并求出最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=ax2+bx+1（a，b为实数），x∈R，
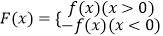
（1）若f（﹣1）=0，且函数f（x）的值域为[0，+∞），求F（x）的表达式；
（2）在（1）的条件下，当x∈[﹣2，2]时，g（x）=f（x）﹣kx是单调函数，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0且f（x）为偶函数，判断F（m）+F（n）能否大于零． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组函数表示同一函数的是（ ）
A.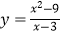
与y=x+3
B.
与y=x﹣1
C.y=x0（x≠0）与y=1（x≠0）
D.y=2x+1，x∈Z与y=2x﹣1，x∈Z -
科目： 来源： 题型：
查看答案和解析>>【题目】[选修4-5：不等式选讲]
已知函数f（x）=|2x﹣1|+|x+1|，g（x）=|x﹣a|+|x+a|．
（Ⅰ）解不等式f（x）＞9；
（Ⅱ）x1∈R，x2∈R，使得f（x1）=g（x2），求实数a的取值范围。
-
科目： 来源： 题型：
查看答案和解析>>【题目】设f（x）是定义在（﹣1，+∞）内的增函数，且f（xy）=f（x）+f（y）若f（3）=1且f（a）＞f（a﹣1）+2
求：
（1）f（9）的值，
（2）求a的取值范围．
相关试题
