搜索
【题目】在等比数列{an}中，a1=1，且a2是a1与a3﹣1的等差中项．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足 
．求数列{bn}的前n项和 
．
参考答案：
【答案】
（1）解：设等比数列{an}的公比为q，
a2是a1与a3﹣1的等差中项，即有a1+a3﹣1=2a2，
即为1+q2﹣1=2q，解得q=2，
即有an=a1qn﹣1=2n﹣1
（2）解： 
=an+ 
=2n﹣1+（ 
﹣ 
），
数列{bn}的前n项和 
=（1+2+22+…+2n﹣1）+（1﹣ 
+ ﹣ 
+ ﹣ 
+…+ ﹣ ）
= 
+1﹣ =2n﹣
【解析】（1）设等比数列{an}的公比为q，运用等差数列的性质和等比数列的通项公式，解方程可得公比q，即可得到所求通项公式；（2）化简bn=2n﹣1+（ ﹣ ），运用分组求和和裂项相消求和，化简即可得到所求和．
【考点精析】利用等比数列的通项公式（及其变式）和数列的前n项和对题目进行判断即可得到答案，需要熟知通项公式：
；数列{an}的前n项和sn与通项an的关系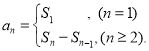
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=cosωx（ω＞0），将y=f（x）的图象向右平移
个单位长度后，所得的图象与原图象重合，则ω的最小值等于 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列{an}满足an+1=qan+2q﹣2（q为常数），若a3 ， a4 ， a5∈{﹣5，﹣2，﹣1，7}，则a1=
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y=f（x）是定义域为R的偶函数． 当x≥0时，f（x）=
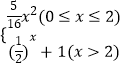，若关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且仅有6个不同实数根，则实数a的取值范围是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某市若规划一居民小区ABCD，AD=2千米，AB=1千米，∠A=90°，政府决定从该地块中划出一个直角三角形地块AEF建活动休闲区（点E，F分别在线段AB，AD上），且该直角三角形AEF的周长为1千米，△AEF的面积为S．
（1）①设AE=x，求S关于x的函数关系式；
②设∠AEF=θ，求S关于θ的函数关系式；
（2）试确定点E的位置，使得直角三角形地块AEF的面积S最大，并求出S的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=
，（a＞0，b∈R）
（1）当x≠0时，求证：f（x）=f（
）；
（2）若函数y=f（x），x∈[
，2]的值域为[5，6]，求f（x）；
（3）在（2）条件下，讨论函数g（x）=f（2x）﹣k（k∈R）的零点个数． -
科目： 来源： 题型：
查看答案和解析>>【题目】设数列{an}，{bn}，{cn}满足a1=a，b1=1，c1=3，对于任意n∈N* ， 有bn+1=
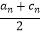，cn+1= 
．
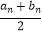（1）求数列{cn﹣bn}的通项公式；
（2）若数列{an}和{bn+cn}都是常数项，求实数a的值；
（3）若数列{an}是公比为a的等比数列，记数列{bn}和{cn}的前n项和分别为Sn和Tn ， 记Mn=2Sn+1﹣Tn ， 求Mn＜
对任意n∈N*恒成立的a的取值范围．
相关试题
