【题目】设数列{an},{bn},{cn}满足a1=a,b1=1,c1=3,对于任意n∈N* , 有bn+1= ![]() ,cn+1=
,cn+1= ![]() .
.
(1)求数列{cn﹣bn}的通项公式;
(2)若数列{an}和{bn+cn}都是常数项,求实数a的值;
(3)若数列{an}是公比为a的等比数列,记数列{bn}和{cn}的前n项和分别为Sn和Tn , 记Mn=2Sn+1﹣Tn , 求Mn< ![]() 对任意n∈N*恒成立的a的取值范围.
对任意n∈N*恒成立的a的取值范围.
参考答案:
【答案】
(1)解:由于bn+1= ![]() ,cn+1=
,cn+1= ![]() .
.
cn+1﹣bn+1= ![]() (bn﹣cn)=﹣
(bn﹣cn)=﹣ ![]() (cn﹣bn),
(cn﹣bn),
即数列{cn﹣bn}是首项为2,公比为﹣ ![]() 的等比数列,
的等比数列,
所以cn﹣bn=2(﹣ ![]() )n﹣1
)n﹣1
(2)解:bn+1+cn+1= ![]() (bn+cn)+an,
(bn+cn)+an,
因为b1+c1=4,数列{an}和{bn+cn}都是常数项,
即有an=a,bn+cn=4,
即4= ![]() ×4+a,解得a=2
×4+a,解得a=2
(3)解:数列{an}是公比为a的等比数列,即有an=an,
由Mn=2Sn+1﹣Tn=2(b1+b2+…+bn)﹣(c1+c2+…+cn)
=2b1+(2b2﹣c1)+(2b3﹣c2)+…+(2bn+1﹣cn)
=2+a+a2+…+an,
由题意可得a≠0且a≠1,0<|a|<1.
由2+ ![]() <
< ![]() 对任意n∈N*恒成立,
对任意n∈N*恒成立,
即有2+ ![]() ≤
≤ ![]() ,
,
解得﹣1<a<0或0<a≤ ![]() .
.
故a的取值范围是(﹣1,0)∪(0, ![]() ]
]
【解析】(1)根据条件建立方程关系即可求出求数列{cn﹣bn}的通项公式;(2)b1+c1=4,数列{an}和{bn+cn}都是常数项,即有an=a,bn+cn=4,即可得到a=2;(3)由等比数列的通项可得an=an , 由Mn=2b1+(2b2﹣c1)+(2b3﹣c2)+…+(2bn+1﹣cn)=2+a+a2+…+an , 由题意可得a≠0且a≠1,0<|a|<1.运用等比数列的求和公式和不等式恒成立思想,计算即可得到a的范围.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系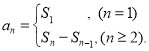 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列{an}中,a1=1,且a2是a1与a3﹣1的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足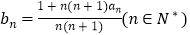 .求数列{bn}的前n项和
.求数列{bn}的前n项和 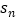 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市若规划一居民小区ABCD,AD=2千米,AB=1千米,∠A=90°,政府决定从该地块中划出一个直角三角形地块AEF建活动休闲区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为1千米,△AEF的面积为S.

(1)①设AE=x,求S关于x的函数关系式;
②设∠AEF=θ,求S关于θ的函数关系式;
(2)试确定点E的位置,使得直角三角形地块AEF的面积S最大,并求出S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 ,(a>0,b∈R)
,(a>0,b∈R)
(1)当x≠0时,求证:f(x)=f( );
);
(2)若函数y=f(x),x∈[ ,2]的值域为[5,6],求f(x);
,2]的值域为[5,6],求f(x);
(3)在(2)条件下,讨论函数g(x)=f(2x)﹣k(k∈R)的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=x2lnx,g(x)=ax3﹣x2 .
(1)求函数f(x)的最小值;
(2)若存在x∈(0,+∞),使f(x)>g(x),求实数a的取值范围;
(3)若使方程f(x)﹣g(x)=0在x∈[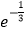 ,en](其中e=2.7…为自然对数的底数)上有解的最小a的值为an , 数列{an}的前n项和为Sn , 求证:Sn<3.
,en](其中e=2.7…为自然对数的底数)上有解的最小a的值为an , 数列{an}的前n项和为Sn , 求证:Sn<3. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,圆C的参数方程
 (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系;
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系;
(1)设M(x,y)是圆C上的动点,求m=3x+4y的取值范围;
(2)求圆C的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】班上有四位同学申请A,B,C三所大学的自主招生,若每位同学只能申请其中一所大学,且申请其中任何一所大学是等可能的.
(1)求恰有2人申请A大学或B大学的概率;
(2)求申请C大学的人数X的分布列与数学期望E(X).
相关试题

