【题目】我国古代数学家刘徽在《九章算术注》中提出割圆术:“割之弥细,所失弥少,割之割,以至于不可割,则与圆合体,而无所失矣”,即通过圆内接正多边形细割圆,并使正多边形的面积无限接近圆的面积,进而来求得较为精确的圆周率.如果用圆的内接正![]() 边形逼近圆,算得圆周率的近似值记为
边形逼近圆,算得圆周率的近似值记为![]() ,那么用圆的内接正
,那么用圆的内接正![]() 边形逼近圆,算得圆周率的近似值加
边形逼近圆,算得圆周率的近似值加![]() 可表示成( )
可表示成( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
设圆的半径为![]() ,由内接正
,由内接正![]() 边形的面积无限接近圆的面积可得:
边形的面积无限接近圆的面积可得:![]() ,由内接正
,由内接正![]() 边形的面积无限接近圆的面积可得:
边形的面积无限接近圆的面积可得:![]() ,问题得解.
,问题得解.
设圆的半径为![]() ,将内接正
,将内接正![]() 边形分成
边形分成![]() 个小三角形,
个小三角形,
由内接正![]() 边形的面积无限接近圆的面积可得:
边形的面积无限接近圆的面积可得:
![]() ,整理得:
,整理得:![]() ,
,
此时![]() ,即:
,即:![]()
同理,由内接正![]() 边形的面积无限接近圆的面积可得:
边形的面积无限接近圆的面积可得:
![]() ,整理得:
,整理得:![]()
此时![]()
所以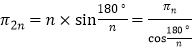
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
(Ⅰ)求证:BC⊥平面ACFE;
(Ⅱ)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
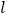 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以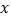 轴正半轴为极轴,建立极坐标系,圆
轴正半轴为极轴,建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.(1)求直线
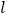 的普通方程和圆
的普通方程和圆 的直角坐标方程;
的直角坐标方程;(2)若点
 是直线
是直线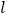 上的动点,过
上的动点,过 作直线与圆
作直线与圆 相切,切点分别为
相切,切点分别为 、
、 ,若使四边形
,若使四边形 的面积最小,求此时点
的面积最小,求此时点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】O为坐标原点,直线l与圆x2+y2=2相切.
(1)若直线l分别与x、y轴正半轴交于A、B两点,求△AOB面积的最小值及面积取得最小值时的直线l的方程.
(2)设直线l交椭圆 =1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
=1于P、Q两点,M为PQ的中点,求|OM|的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】几个孩子在一棵枯树上玩耍,他们均不慎失足下落.已知
(
 )甲在下落的过程中依次撞击到树枝
)甲在下落的过程中依次撞击到树枝 ,
, ,
,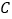 ;
;(
 )乙在下落的过程中依次撞击到树枝
)乙在下落的过程中依次撞击到树枝 ,
, ,
,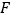 ;
;(
 )丙在下落的过程中依次撞击到树枝
)丙在下落的过程中依次撞击到树枝 ,
, ,
,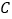 ;
;(
 )丁在下落的过程中依次撞击到树枝
)丁在下落的过程中依次撞击到树枝 ,
, ,
, ;
;(
 )戊在下落的过程中依次撞击到树枝
)戊在下落的过程中依次撞击到树枝 ,
,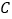 ,
, .
.倒霉和李华在下落的过程中撞到了从
 到
到 的所有树枝,根据以上信息,在李华下落的过程中,和这
的所有树枝,根据以上信息,在李华下落的过程中,和这 根树枝不同的撞击次序有( )种.
根树枝不同的撞击次序有( )种.A.
 B.
B.  C.
C.  D.
D. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
 中,侧面对角线
中,侧面对角线 ,
, 上分别有一点E,F,且
上分别有一点E,F,且 ,则直线EF与平面ABCD所成的角的大小为( )
,则直线EF与平面ABCD所成的角的大小为( )
A.0°B.60°C.45°D.30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是正三角形,EA,CD都垂直于平面ABC,且
是正三角形,EA,CD都垂直于平面ABC,且 ,
, ,F是BE的中点,
,F是BE的中点,
求证:(1)
 平面ABC;
平面ABC;(2)
 平面EDB.
平面EDB.(3)求几何体
 的体积.
的体积.
相关试题

