【题目】已知函数f(x)= ![]() (m,n为常数)是定义在[﹣1,1]上的奇函数,且f(﹣1)=﹣
(m,n为常数)是定义在[﹣1,1]上的奇函数,且f(﹣1)=﹣ ![]() .
.
(1)求函数f(x)的解析式;
(2)解关于x的不等式f(2x﹣1)<﹣f(x).
参考答案:
【答案】
(1)解:由于函数f(x)= ![]() (m,n为常数)是定义在[﹣1,1]上的奇函数,
(m,n为常数)是定义在[﹣1,1]上的奇函数,
∴f(0)= ![]() =0,∴n=0,
=0,∴n=0,
再根据f(﹣1)= ![]() =﹣
=﹣ ![]() ,∴m=1,
,∴m=1,
∴f(x)= ![]() =
= ![]()
(2)解:关于x的不等式f(2x﹣1)<﹣f(x)=﹣f(x),
∵f(x)= ![]() 在(0,1]上单调递增,∴f(x)在[﹣1,1]上单调递增.
在(0,1]上单调递增,∴f(x)在[﹣1,1]上单调递增.
故由不等式可得 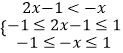 ,求得0≤x<
,求得0≤x< ![]() ,
,
故不等式的解集为{x|0≤x< ![]() }
}
【解析】(1)由f(0)= ![]() =0,求得n=0,再根据f(﹣1)=﹣
=0,求得n=0,再根据f(﹣1)=﹣ ![]() ,求得m=1,∴f(x)得解析式.(2)关于x的不等式即f(2x﹣1)<﹣f(x),再根据f(x)在[﹣1,1]上单调递增,可得不等式组
,求得m=1,∴f(x)得解析式.(2)关于x的不等式即f(2x﹣1)<﹣f(x),再根据f(x)在[﹣1,1]上单调递增,可得不等式组 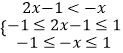 ,由此求得x的范围.
,由此求得x的范围.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在长方体ABCD﹣A1B1C1D1中,E、M、N分别是BC、AE、D1C的中点,AD=AA1 , AB=2AD
(Ⅰ)证明:MN∥平面ADD1A1
(Ⅱ)求直线AD与平面DMN所成角的余弦值.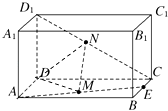
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(4,2)是直线l被椭圆
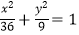 所截得的线段的中点,
所截得的线段的中点,
(1)求直线l的方程
(2)求直线l被椭圆截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
,  分别是
分别是 中点,弧
中点,弧 的半径分别为
的半径分别为 ,点
,点 平分弧
平分弧 ,过点
,过点 作弧
作弧 的切线分别交
的切线分别交 于点
于点 .四边形
.四边形 为矩形,其中点
为矩形,其中点 在线段
在线段 上,点
上,点 在弧
在弧 上,延长
上,延长 与
与 交于点
交于点 .设
.设 ,矩形
,矩形 的面积为
的面积为 .
.(1)求
 的解析式并求其定义域;
的解析式并求其定义域;(2)求
 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
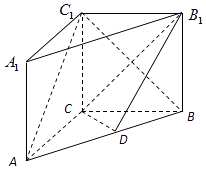
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求二面角B﹣DC﹣B1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
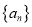 的前
的前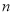 项和为
项和为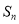 ,且
,且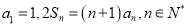 .令
.令 .
.(1)求
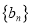 的通项公式;
的通项公式;(2)若
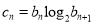 ,且数列
,且数列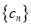 的前
的前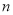 项和为
项和为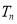 ,求
,求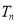 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2﹣
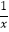 (x>0),若存在实数m、n(m<n)使f(x)在区间(m,n)上的值域为(tm,tn),则实数t的取值范围是 .
(x>0),若存在实数m、n(m<n)使f(x)在区间(m,n)上的值域为(tm,tn),则实数t的取值范围是 .
相关试题

