【题目】已知函数φ(x)= ![]() ,a>0
,a>0
(1)若函数f(x)=lnx+φ(x),在(1,2)上只有一个极值点,求a的取值范围;
(2)若g(x)=|lnx|+φ(x),且对任意x1 , x2∈(0,2],且x1≠x2 , 都有 ![]() <﹣1,求a的取值范围.
<﹣1,求a的取值范围.
参考答案:
【答案】
(1)解: f(x)=lnx+φ(x)=lnx+ ![]() ,(x>0,a>0),
,(x>0,a>0),
f′(x)= ![]() ﹣
﹣ ![]() ,
,
当f′(1)f′(2)<0时,函数f(x)在区间(1,2)上只有一个极值点,
即为(1﹣ ![]() a)(
a)( ![]() ﹣
﹣ ![]() a)<0,
a)<0,
解得:4<a< ![]() ;
;
(2)解:∵ ![]() <﹣1,
<﹣1,
∴有 ![]() +1<0,
+1<0,
∴ ![]() <0,
<0,
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数.
当1≤x≤2时,h(x)=lnx+ ![]() +x,h′(x)=
+x,h′(x)= ![]() ﹣
﹣ ![]() +1,
+1,
令h′(x)≤0,得:a≥ ![]() +(x+1)2=x2+3x+
+(x+1)2=x2+3x+ ![]() +3对x∈[1,2]恒成立,
+3对x∈[1,2]恒成立,
设m(x)=x2+3x+ ![]() +3,则m′(x)=2x+3﹣
+3,则m′(x)=2x+3﹣ ![]() ,
,
∵1≤x≤2,∴m′(x)=2x+3﹣ ![]() >0,
>0,
∴m(x)在[1,2]上递增,则当x=2时,m(x)有最大值为 ![]() ,
,
∴a≥ ![]() ;
;
当0<x<1时,h(x)=﹣lnx+ ![]() +x,h′(x)=﹣
+x,h′(x)=﹣ ![]() ﹣
﹣ ![]() +1,
+1,
令h′(x)≤0,得:a≥﹣ ![]() +(x+1)2=x2+x﹣
+(x+1)2=x2+x﹣ ![]() ﹣1,
﹣1,
设t(x)=x2+x﹣ ![]() ﹣1,则t′(x)=2x+1+
﹣1,则t′(x)=2x+1+ ![]() >0,
>0,
∴t(x)在(0,1)上是增函数,
∴t(x)<t(1)=0,
∴a≥0
【解析】(1)求出函数的导数,得到f′(1)f′(2)<0,解出即可;(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,侧面
,侧面 底面
底面 .
.
(1)求证:平面
 平面
平面 ;
;(2)若
 ,且二面角
,且二面角 等于
等于 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
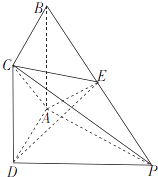
(1)证明:AC⊥DE;
(2)若PC=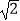 BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个定点
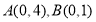 ,动点
,动点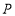 满足
满足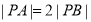 .设动点
.设动点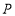 的轨迹为曲线
的轨迹为曲线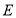 ,直线
,直线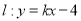 .
.(1)求曲线
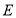 的轨迹方程;
的轨迹方程;(2)若
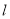 与曲线
与曲线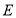 交于不同的
交于不同的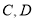 两点,且
两点,且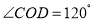 (
(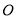 为坐标原点),求直线
为坐标原点),求直线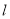 的斜率;
的斜率;(3)若
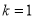 ,
, 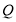 是直线
是直线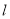 上的动点,过
上的动点,过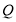 作曲线
作曲线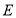 的两条切线
的两条切线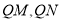 ,切点为
,切点为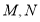 ,探究:直线
,探究:直线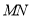 是否过定点.
是否过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.

(1)求证:ABDE=BCCE;
(2)若AB=8,BC=4,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是
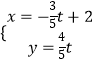 (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的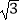 倍,求a的值.
倍,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 底面
底面 ,底面
,底面 为矩形,
为矩形, 为
为 的中点,且
的中点,且 ,
, ,
, .
.
(1)求证:
 平面
平面 ;
;(2)若点
 为线段
为线段 上一点,且
上一点,且 ,求四棱锥
,求四棱锥 的体积.
的体积.
相关试题

