【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
参考答案:
【答案】(Ⅰ)P=![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)根据分层抽样原理计算抽取的男、女生人数,利用列举法计算基本事件数,求出对应的概率值;
(2)由频率分布直方图计算对应的数据,填写列联表,计算![]() 值,对照数表即可得出概率结论.
值,对照数表即可得出概率结论.
试题解析:(Ⅰ)由已知得,抽取的100名学生中,男生60名,女生40名,
分数小于等于110分的学生中,男生人有60×0.05=3(人),记为A1,A2,A3;
女生有40×0.05=2(人),记为B1,B2; ………………2分
从中随机抽取2名学生,所有的可能结果共有10种,它们是:
(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2);
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:
(A1,B1),(A1,B2),(A2,B1),
(A2,B2),(A3,B1),(A3,B2);
故所求的概率为P=![]() .
.
(Ⅱ)由频率分布直方图可知,
在抽取的100名学生中,男生 60×0.25=15(人),女生40×0.375=15(人); …7分
据此可得2×2列联表如下:
数学尖子生 | 非数学尖子生 | 合计 | |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
(9分)
所以得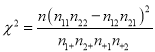
![]() ;
;
因为1.79<2.706,
所以没有90%的把握认为“数学尖子生与性别有关”
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
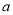 为实数,函数
为实数,函数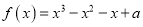 .
.(1)求
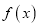 的极值;
的极值;(2)当
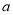 在什么范围内取值时,曲线
在什么范围内取值时,曲线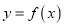 与
与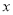 轴仅有一个交点?
轴仅有一个交点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四棱锥
 的底面为直角梯形,
的底面为直角梯形,  .点
.点 是
是 的中点.
的中点.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)已知平面
 底面
底面 ,且
,且 .在棱
.在棱 上是否存在点
上是否存在点 ,使
,使 ?请说明理由.
?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)由数字1、2、3、4、5、6、7组成无重复数字的七位数
求三个偶数必相邻的七位数的个数及三个偶数互不相邻的七位数的个数
(2)六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?
(I)每组两本
(II)一组一本,一组二本,一组三本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出一份
 道题的数学试卷,试卷内的
道题的数学试卷,试卷内的 道题是这样产生的:从含有
道题是这样产生的:从含有 道选择题的题库中随机抽
道选择题的题库中随机抽 道;从
道;从 道填空题的题库中随机抽
道填空题的题库中随机抽 道;从
道;从 道解答题的题库中随机抽
道解答题的题库中随机抽 道.使用合适的方法确定这套试卷的序号(选择题编号为
道.使用合适的方法确定这套试卷的序号(选择题编号为 ,填空题编号为
,填空题编号为 ,解答题编号为
,解答题编号为 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个学生在一次竞赛中要回答
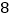 道题是这样产生的:从
道题是这样产生的:从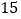 道物理题中随机抽取
道物理题中随机抽取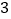 道;从
道;从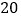 道化学题中随机抽取
道化学题中随机抽取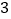 道;从
道;从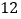 道生物题中随机抽取
道生物题中随机抽取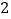 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为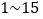 ,化学题的编号为
,化学题的编号为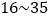 ,生物题的编号为
,生物题的编号为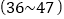 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率低于
 ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

