【题目】设f(x)=a﹣ ![]() ,x∈R,(其中a为常数).
,x∈R,(其中a为常数).
(1)若f(x)为奇函数,求a的值;
(2)若不等式f(x)+a>0恒成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:法一:(1因为f(x)为奇函数
所以f(﹣x)=﹣f(x)
即: ![]()
所以a=1
法二:因为x∈R,f(x)为奇函数
所以f(﹣x)=﹣f(x)
所以f(﹣0)=﹣f(0)
所以f(0)=0
得:a=1
(2)解: ![]()
因为f(x)+a>0恒成立,
即 ![]() 恒成立.
恒成立.
因为2x+1>1,
所以 ![]() .
.
所以2a≥2
即a≥1
【解析】(1)法一:利用函数的奇偶性的定义,直接求解即可.
法二:求出f(0)=0代入求解即可.(2)利用函数恒成立,分离变量,利用函数的值域求解即可.
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷
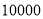 份,
份,  名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).(1)要从这
 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取 名中小学生进一步调查,则在
名中小学生进一步调查,则在 (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?(2)若希望
 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于 (小时),请估计
(小时),请估计 的值,并说明理由.
的值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 且
且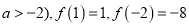 ,且,函数
,且,函数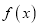 的图象与直线
的图象与直线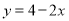 相切.
相切.(1)求
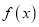 的解析式;
的解析式;(2)若当
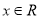 时,
时, 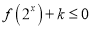 恒成立,求实数
恒成立,求实数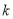 的取值范围;
的取值范围;(3)是否存在区间
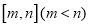 ,使得
,使得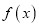 在区间
在区间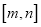 上的值域恰好为
上的值域恰好为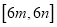 ?若存在,请求出区间
?若存在,请求出区间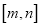 ,若不存在,请说明理由.
,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
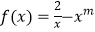 ,且
,且 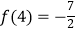 .
.
(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并给予证明;
(3)求函数f(x)在区间[﹣5,﹣1]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家环保部最新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别
PM2.5平均浓度
频数
频率
第一组
(0,25]
3
0.15
第二组
(25,50]
12
0.6
第三组
(50,75]
3
0.15
第四组
(75,100]
2
0.1
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(II)求样本平均数,并根据样本估计总计的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的两个焦点是
的两个焦点是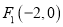 ,
, 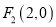 ,且椭圆
,且椭圆 经过点
经过点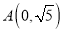 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若过椭圆
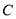 的左焦点
的左焦点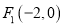 且斜率为1的直线
且斜率为1的直线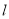 与椭圆
与椭圆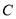 交于
交于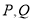 两点,求线段
两点,求线段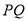 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
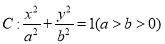 的右焦点为
的右焦点为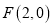 ,点
,点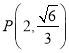 在椭圆上.
在椭圆上.(1)求椭圆
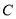 的方程;
的方程;(2)过点
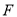 的直线
的直线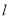 ,交椭圆
,交椭圆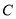 于
于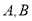 两点,点
两点,点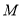 在椭圆
在椭圆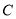 上,坐标原点
上,坐标原点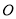 恰为
恰为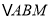 的重心,求直线
的重心,求直线 的方程.
的方程.
相关试题

