【题目】设△ABC的内角A,B,C所对边分别为a,b,c,且a+c=6,b=2, ![]() .
.
(1)求a,c的值;
(2)求sin(A﹣B)的值.
参考答案:
【答案】
(1)解:∵a+c=6①,b=2,cosB= ![]() ,
,
∴由余弦定理得:b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣ ![]() ac=36﹣
ac=36﹣ ![]() ac=4,
ac=4,
整理得:ac=9②,
联立①②解得:a=c=3;
(2)解:∵cosB= ![]() ,B为三角形的内角,
,B为三角形的内角,
∴sinB= ![]() =
= ![]() ,
,
∵b=2,a=3,sinB= ![]() ,
,
∴由正弦定理得:sinA= ![]() =
= ![]() =
= ![]() ,
,
∵a=c,即A=C,∴A为锐角,
∴cosA= ![]() =
= ![]() ,
,
则sin(A﹣B)=sinAcosB﹣cosAsinB= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]()
【解析】(1)利用余弦定理列出关系式,将b与cosB的值代入,利用完全平方公式变形,求出acb的值,与a+c的值联立即可求出a与c的值即可;(2)先由cosB的值,利用同角三角函数间的基本关系求出sinB的值,再由a,b及sinB的值,利用正弦定理求出sinA的值,进而求出cosA的值,所求式子利用两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出值.
【考点精析】本题主要考查了两角和与差的正弦公式和正弦定理的定义的相关知识点,需要掌握两角和与差的正弦公式:![]() ;正弦定理:
;正弦定理:![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2019年举行促销活动,经过调查测算,该产品的年销量(即该厂的年产量)
 (单位:万件)与年促销费用
(单位:万件)与年促销费用 (
( )(单位:万元)满足
)(单位:万元)满足 (
( 为常数),如果不搞促销活动,则该产品的年销量只能是1万件. 已知2019年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).
为常数),如果不搞促销活动,则该产品的年销量只能是1万件. 已知2019年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).(1)将该厂家2019年该产品的利润
 万元表示为年促销费用
万元表示为年促销费用 万元的函数;
万元的函数;(2)该厂家2019年的年促销费用投入多少万元时,厂家利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)当
 时,函数
时,函数 的图象恒不在
的图象恒不在 轴的上方,求实数
轴的上方,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义“正对数”:ln+x=
 ,现有四个命题:
,现有四个命题:
①若a>0,b>0,则ln+(ab)=bln+a;
②若a>0,b>0,则ln+(ab)=ln+a+ln+b;
③若a>0,b>0,则 ;
;
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2.
其中的真命题有(写出所有真命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】ΔABC的内角A,B,C的对边分别为a,b,c,根据下列条件解三角形,其中有两解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4
 ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30° -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数,
为参数, ),以坐标原点为极点,以
),以坐标原点为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)已知曲线
 和曲线
和曲线 交于
交于 ,
, 两点(
两点( 在
在 、
、 之间),且
之间),且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
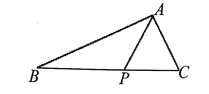
查看答案和解析>>【题目】如图,在
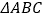 中,点
中,点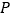 在
在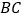 边上,
边上, ,
,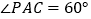 ,
,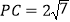 ,
,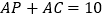 .
.
(1)求
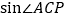 的值;
的值;(2)若
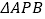 的面积是
的面积是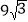 ,求
,求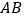 的长.
的长.
相关试题

