【题目】定义“正对数”:ln+x= ![]() ,现有四个命题:
,现有四个命题:
①若a>0,b>0,则ln+(ab)=bln+a;
②若a>0,b>0,则ln+(ab)=ln+a+ln+b;
③若a>0,b>0,则 ![]() ;
;
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2.
其中的真命题有(写出所有真命题的序号)
参考答案:
【答案】①③④
【解析】解:(1)对于①,由定义,当a≥1时,ab≥1,故ln+(ab)=ln(ab)=blna,又bln+a=blna,故有ln+(ab)=bln+a;当a<1时,ab<1,故ln+(ab)=0,又a<1时bln+a=0,所以此时亦有ln+(ab)=bln+a,故①正确;
(2)对于②,此命题不成立,可令a=2,b= ![]() ,则ab=
,则ab= ![]() ,由定义ln+(ab)=0,ln+a+ln+b=ln2,所以ln+(ab)≠ln+a+ln+b,故②错误;
,由定义ln+(ab)=0,ln+a+ln+b=ln2,所以ln+(ab)≠ln+a+ln+b,故②错误;
(3)对于③,
i. ![]() ≥1时,此时
≥1时,此时 ![]() ≥0,
≥0,
当a≥b≥1时,ln+a﹣ln+b=lna﹣lnb= ![]() ,此时则
,此时则 ![]() ,命题成立;
,命题成立;
当a>1>b>0时,ln+a﹣ln+b=lna,此时 ![]() ,
, ![]() >lna,则
>lna,则 ![]() ,命题成立;
,命题成立;
当1>a≥b>0时,ln+a﹣ln+b=0, ![]() 成立;
成立;
ii. ![]() <1时,同理可验证是正确的,故③正确;
<1时,同理可验证是正确的,故③正确;
(4)对于④,
当a≥1,b≥1时,ln+(a+b)=ln(a+b),ln+a+ln+b+ln2=lna+lnb+ln2=ln(2ab),
∵a+b﹣2ab=a﹣ab+b﹣ab=a(1﹣b)+b(1﹣a)≤0,
∴a+b≤2ab,
∴ln(a+b)<ln(2ab),
∴ln+(a+b)≤ln+a+ln+b+ln2.
当a>1,0<b<1时,ln+(a+b)=ln(a+b),ln+a+ln+b+ln2=lna+ln2=ln(2a),
∵a+b﹣2a=b﹣a≤0,
∴a+b≤2a,
∴ln(a+b)<ln(2a),
∴ln+(a+b)≤ln+a+ln+b+ln2.
当b>1,0<a<1时,同理可证ln+(a+b)≤ln+a+ln+b+ln2.
当0<a<1,0<b<1时,可分a+b≥1和a+b<1两种情况,均有ln+(a+b)≤ln+a+ln+b+ln2.
故④正确.
所以答案是①③④.
【考点精析】关于本题考查的命题的真假判断与应用,需要了解两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数
 的定义域为
的定义域为 .
.(1)求实数
 ,
, 的值;
的值;(2)判断函数
 的单调性,若实数
的单调性,若实数 满足
满足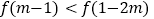 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2019年举行促销活动,经过调查测算,该产品的年销量(即该厂的年产量)
 (单位:万件)与年促销费用
(单位:万件)与年促销费用 (
( )(单位:万元)满足
)(单位:万元)满足 (
( 为常数),如果不搞促销活动,则该产品的年销量只能是1万件. 已知2019年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).
为常数),如果不搞促销活动,则该产品的年销量只能是1万件. 已知2019年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).(1)将该厂家2019年该产品的利润
 万元表示为年促销费用
万元表示为年促销费用 万元的函数;
万元的函数;(2)该厂家2019年的年促销费用投入多少万元时,厂家利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)当
 时,函数
时,函数 的图象恒不在
的图象恒不在 轴的上方,求实数
轴的上方,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C所对边分别为a,b,c,且a+c=6,b=2,
 .
.
(1)求a,c的值;
(2)求sin(A﹣B)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】ΔABC的内角A,B,C的对边分别为a,b,c,根据下列条件解三角形,其中有两解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4
 ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30° -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数,
为参数, ),以坐标原点为极点,以
),以坐标原点为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)已知曲线
 和曲线
和曲线 交于
交于 ,
, 两点(
两点( 在
在 、
、 之间),且
之间),且 ,求实数
,求实数 的值.
的值.
相关试题

