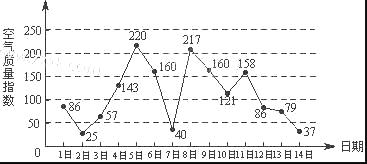
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)从3月5日开始连续三天的空气质量指数方差最大
(Ⅲ)从3月5日开始连续三天的空气质量指数方差最大
【解析】(Ⅰ)在3月1日至3月13日这13天中,1日,2日,3日,7日,12日,13日共6天的空气质量优良,所以此人到达当日空气质量优良的概率为![]() 。
。
(Ⅱ)根据题意,事件“此人在该市停留期间只有1天空气重度污染”等价于“此人到达该市的日期是4日,或5日,或7日,或8日”,
所以此人在该市停留期间只有1天空气重度污染的概率是![]() 。
。
(Ⅲ)从3月5日开始连续三天的空气质量指数方差最大.
本题主要考查的是古典概率。由图读出基本事件的总数和满足条件的事件个数,代入古典概型公式计算即可。连续三天的空气质量指数方差最大的是应该是这三天空气质量指数悬殊最大的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为
 ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将
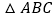 沿DE,EF,DF折成正四面体
沿DE,EF,DF折成正四面体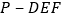 ,则在此正四面体中,下列说法正确的是______.
,则在此正四面体中,下列说法正确的是______.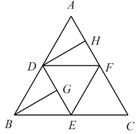
 异面直线PG与DH所成的角的余弦值为
异面直线PG与DH所成的角的余弦值为 ;
;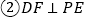 ;
;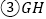 与PD所成的角为
与PD所成的角为 ;
;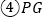 与EF所成角为
与EF所成角为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校书法兴趣组有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级
二年级
三年级
男同学
A
B
C
女同学
X
Y
Z
现从这6名同学中随机选出2人参加书法比赛
 每人被选到的可能性相同
每人被选到的可能性相同 .
.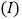 用表中字母列举出所有可能的结果;
用表中字母列举出所有可能的结果;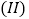 设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,设f(n)=an , 且f(n)满足f(n+1)﹣2f(n)=2n(n∈N*),且a1=1.
(1)设 ,证明数列{bn}为等差数列;
,证明数列{bn}为等差数列;
(2)求数列{an}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,
 ,E、F分别为AD、PC中点.
,E、F分别为AD、PC中点. 
(1)求点F到平面PAB的距离;
(2)求证:平面PCE⊥平面PBC;
(3)求二面角E﹣PC﹣D的大小. -
科目: 来源: 题型:
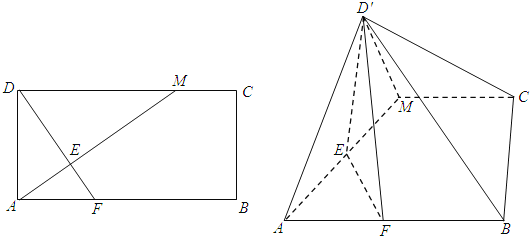
查看答案和解析>>【题目】如图,在矩形ABCD中,
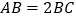 ,点M在边DC上,点F在边AB上,且
,点M在边DC上,点F在边AB上,且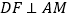 ,垂足为E,若将
,垂足为E,若将 沿AM折起,使点D位于
沿AM折起,使点D位于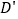 位置,连接
位置,连接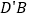 ,
,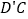 得四棱锥
得四棱锥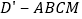 .
.
 Ⅰ
Ⅰ 求证:
求证: ;
; Ⅱ
Ⅱ 若
若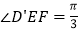 ,直线
,直线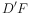 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为 ,求直线
,求直线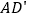 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.
相关试题

