【题目】已知数列{an}的前n项和为Sn , 通项公式为 ![]() .
.
(Ⅰ)计算f(1),f(2),f(3)的值;
(Ⅱ)比较f(n)与1的大小,并用数学归纳法证明你的结论.
参考答案:
【答案】解:(Ⅰ)由已知 ![]() ,
, ![]() ,
, ![]() ;
;
(Ⅱ)由(Ⅰ)知f(1)>1,f(2)>1;当n≥3时,猜想:f(n)<1.
下面用数学归纳法证明:
①由(Ⅰ)当n=3时,f(n)<1;
②假设n=k(k≥3)时,f(n)<1,即 ![]() ,那么
,那么 ![]() =
= ![]()
![]() =
= ![]() =
= ![]() ,
,
所以当n=k+1时,f(n)<1也成立.由(1)和(2)知,当n≥3时,f(n)<1.
所以当n=1,和n=2时,f(n)>1;当n≥3时,f(n)<1
【解析】(1)此问根据通项公式计算出前n项的和.当n=1时,f(1)=s2;当n=2时,f(2)=s4﹣s1=a2+a3;当n=3时,f(3)=s6﹣s2 . (2)当n=1时, ![]() ≥1.当n≥2时,f(n)中没有a1 , 因此都小于1.
≥1.当n≥2时,f(n)中没有a1 , 因此都小于1.
【考点精析】认真审题,首先需要了解数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3﹣bx2+cx+b﹣a(a>0).
(1)设c=0. ①若a=b,曲线y=f(x)在x=x0处的切线过点(1,0),求x0的值;
②若a>b,求f(x)在区间[0,1]上的最大值.
(2)设f(x)在x=x1 , x=x2两处取得极值,求证:f(x1)=x1 , f(x2)=x2不同时成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}和{bn}的项数均为m,则将数列{an}和{bn}的距离定义为
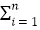 |ai﹣bi|.
|ai﹣bi|.
(1)给出数列1,3,5,6和数列2,3,10,7的距离;
(2)设A为满足递推关系an+1=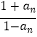 的所有数列{an}的集合,{bn}和{cn}为A中的两个元素,且项数均为m,若b1=2,c1=3,{bn}和{cn}的距离小于2016,求m的最大值;
的所有数列{an}的集合,{bn}和{cn}为A中的两个元素,且项数均为m,若b1=2,c1=3,{bn}和{cn}的距离小于2016,求m的最大值;
(3)记S是所有7项数列{an|1≤n≤7,an=0或1}的集合,TS,且T中任何两个元素的距离大于或等于3,证明:T中的元素个数小于或等于16. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合M={1,2…9}中抽取3个不同的数构成集合{a1 , a2 , a3}
(1)对任意i≠j,求满足|ai﹣aj|≥2的概率;
(2)若a1 , a2 , a3成等差数列,设公差为ξ(ξ>0),求ξ的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列几个命题:
①命题p:任意x∈R,都有cosx≤1,则¬p:存在x0∈R,使得cosx0≤1
②命题“若a>2且b>2,则a+b>4且ab>4”的逆命题为假命题
③空间任意一点O和三点A,B,C,则 =3
=3 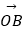 =2
=2  是A,B,C三点共线的充分不必要条件
是A,B,C三点共线的充分不必要条件
④线性回归方程y=bx+a对应的直线一定经过其样本数据点(x1 , y1),(x2 , y2),…,(xn , yn)中的一个
其中不正确的个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数y=f(x)的一对“友好点对”(点对(P,Q)与(Q,P)看作同一对“友好点对”).已知函数f(x)=
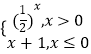 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.3对
B.2对
C.1对
D.0对
相关试题

