【题目】如图,在平面直角坐标系![]() 中,椭圆:
中,椭圆: ![]() 的离心率为
的离心率为![]() ,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 已知椭圆的上顶点为A,点B,C是上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() .
.
① 求证: ![]() 为定值;
为定值;
② 求△CEF的面积的最小值.

参考答案:
【答案】(Ⅰ)![]() (Ⅱ)①详见解析②
(Ⅱ)①详见解析②![]()
【解析】试题分析:
(1)由题意求得![]() 的值,结合椭圆焦点位于
的值,结合椭圆焦点位于![]() 轴上写出标准方程即可;
轴上写出标准方程即可;
(2)①中,分别求得![]() 的值,然后求解其乘积即可证得结论;
的值,然后求解其乘积即可证得结论;
②中,联立直线与椭圆的方程,利用面积公式得出三角形面积的解析式,最后利用均值不等式求得面积的最小值即可.
试题解析:
(Ⅰ)由题知![]() ,由
,由![]() ,
,
所以![]() .
.
故椭圆的方程为![]() .
.
(Ⅱ)① 证法一:设![]() ,则
,则![]() ,
,
因为点B,C关于原点对称,则![]() ,
,
所以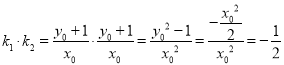 .
.
证法二:直线AC的方程为![]() ,
,
由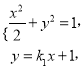 得
得![]() ,
,
解得![]() ,同理
,同理![]() ,
,
因为B,O,C三点共线,则由![]() ,
,
整理得![]() ,
,
所以![]() .
.
②直线AC的方程为![]() ,直线AB的方程为
,直线AB的方程为![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
令y=2,得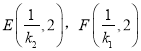 ,
,
而![]() ,
,
所以,△CEF的面积![]()
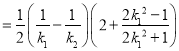
![]() .
.
由![]() 得
得![]() ,
,
则![]()
![]() ,当且仅当
,当且仅当![]() 取得等号,
取得等号,
所以△CEF的面积的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
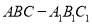 中,侧棱
中,侧棱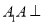 平面
平面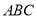 ,
, 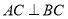 ,
, 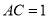 ,
, 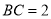 ,
, 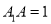 ,点
,点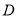 是
是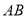 的中点
的中点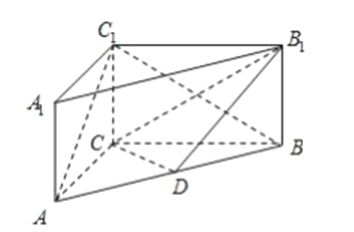
(1)证明:
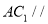 平面
平面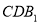 ;
;(2)在线段
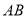 上找一点
上找一点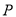 ,使得直线
,使得直线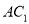 与
与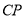 所成角的为
所成角的为 ,求
,求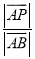 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x∈R|ax2+2x+1=0,a∈R}中只有一个元素,求a的值并求出这个元素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?
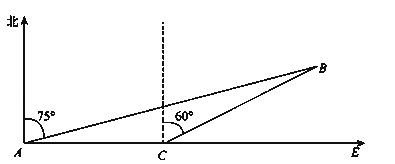
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
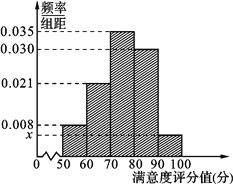
(Ⅰ) 求图中
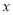 的值;
的值;(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取2人进行座谈,求所抽取的两人中至少有一名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分别求出适合下列条件的直线方程:
(Ⅰ)经过点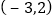 且在x轴上的截距等于在y轴上截距的2倍;
且在x轴上的截距等于在y轴上截距的2倍;
(Ⅱ)经过直线2x+7y﹣4=0与7x﹣21y﹣1=0的交点,且和A(﹣3,1),B(5,7)等距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为
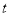 件时,销售所得的收入为
件时,销售所得的收入为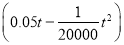 万元.
万元.(1)该公司这种产品的年生产量为
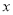 件,生产并销售这种产品所得到的利润关于当年产量
件,生产并销售这种产品所得到的利润关于当年产量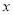 的函数为
的函数为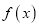 ,求
,求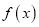 ;
;(2)当该公司的年产量为多少件时,当年所获得利润最大?
相关试题

