【题目】已知函数f(x)=( ![]() )x , 函数g(x)=log
)x , 函数g(x)=log ![]() x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( ![]() )t+1 , (
)t+1 , ( ![]() )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log ![]() f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
参考答案:
【答案】
(1)解: ![]() 定义域为R;
定义域为R;
所以ax2+2x+1>0对一切x∈R成立;
当a=0时,2x+1>0不可能对一切x∈R成立;
所以 ![]() 即:
即: ![]() ;
;
综上 a>1
(2)解: ![]() ;
;
令 ![]() ;
;
所以y=u2﹣2u+2=(u﹣1)2+1,u∈[t,t+1];
当t≥1时, ![]() ;
;
当0<t<1时,ymin=1;
当t≤0时, ![]() ;
;
所以 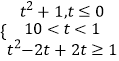
(3)解:y=x2在[0,+∞)上是增函数;
若存在非负实数m、n满足题意,则 ![]() ;
;
即m、n是方程x2=2x的两非负实根,且m<n;
所以m=0,n=2;
即存在m=0,n=2满足题意
【解析】(1)g(ax2+2x+1)的定义域为R,即所以ax2+2x+1>0对一切x∈R成立,转化为一元二次函数问题;(2)利用换元法构造新函数y=u2﹣2u+2=(u﹣1)2+1,u∈[t,t+1];对参数t分类讨论其位置,判断函数的最小值即可;(3)根据函数的单调性,列出方程组 ![]() ,转化为:即m、n是方程x2=2x的两非负实根,且m<n;
,转化为:即m、n是方程x2=2x的两非负实根,且m<n;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:
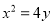 ,过点
,过点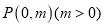 的动直线l与C相交于
的动直线l与C相交于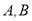 两点,抛物线C在点A和点B处的切线相交于点Q.
两点,抛物线C在点A和点B处的切线相交于点Q.(Ⅰ)写出抛物线的焦点坐标和准线方程;
(Ⅱ)求证:点Q在直线
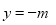 上;
上; 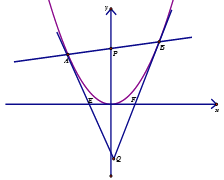
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
 的定义域为( )
的定义域为( )
A.(﹣1,1]
B.(﹣1,0)∪(0,1]
C.(﹣1,1)
D.(﹣1,0)∪(0,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
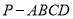 中,
中, 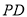 ⊥底面
⊥底面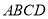 ,
, 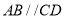 ,
, 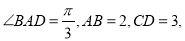
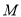 为
为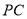 上一点
上一点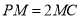 .
.(1)证明:
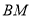 ∥平面
∥平面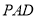 ;
;若
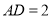 ,
, 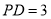 ,求二面角
,求二面角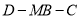 的正弦值.
的正弦值.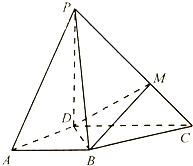
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合U={x|x是小于6的正整数},A={1,2},B∩(C∪A)={4},则∪(A∪B)=( )
A.{3,5}
B.{3,4}
C.{2,3}
D.{2,4} -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,经过点
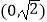 且斜率为k的直线l与椭圆
且斜率为k的直线l与椭圆 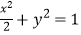 有两个不同的交点P和Q.
有两个不同的交点P和Q.
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量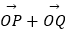 与
与 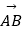 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合M={f(x)|f2(x)﹣f2(y)=f(x+y)f(x﹣y),x,y∈R},有下列命题
①若f(x)= ,则f(x)∈M;
,则f(x)∈M;
②若f(x)=2x,则f(x)∈M;
③f(x)∈M,则y=f(x)的图象关于原点对称;
④f(x)∈M,则对于任意实数x1 , x2(x1≠x2),总有 <0成立;
<0成立;
其中所有正确命题的序号是 . (写出所有正确命题的序号)
相关试题

