【题目】已知函数![]()
(1)求![]() 的最小正周期和递减区间;
的最小正周期和递减区间;
(2)当![]() 时,求
时,求![]() 的最大值和最小值,以及取得最值时
的最大值和最小值,以及取得最值时![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)由已知化简得![]() , 得函数的最小正周期
, 得函数的最小正周期![]() ,令
,令
令![]() ,即可求解函数的单调递减区间;
,即可求解函数的单调递减区间;
(2)由(1)得函数![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增,即可求解函数最大值与最小值.
上单调递增,即可求解函数最大值与最小值.
详解:(1)由已知,有f(x)=cosx(![]() sinx+
sinx+![]() cosx)-
cosx)-![]() cos2x+
cos2x+![]() =
=![]() sinxcosx-
sinxcosx-![]() cos2x+
cos2x+![]()
=![]() sin2x-
sin2x-![]() (1+cos2x)+
(1+cos2x)+![]() =
=![]() sin2x-
sin2x-![]() cos2x=
cos2x=![]() sin(2x-
sin(2x-![]() )
)
![]()
![]() , 所以f(x)的最小正周期
, 所以f(x)的最小正周期![]() .
.
令![]() ,得
,得![]() ,
,
所以f(x)的单调递减区间为![]() .
.
(2)因为f(x)在区间[-![]() ,-
,-![]() ]上是减函数,在区间[-
]上是减函数,在区间[-![]() ,
,![]() ]上是增函数,
]上是增函数,
f(-![]() )=-
)=-![]() ,f(-
,f(-![]() )=-
)=-![]() ,f(
,f(![]() )=
)=![]() ,
,
所以,函数f(x)在闭区间[-![]() ,
,![]() ]上的最大值为
]上的最大值为![]() ,此时
,此时![]() ,
,
最小值为-![]() ,此时
,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为  ,
,  ,
,  ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用  表示乙队的总得分.
表示乙队的总得分.
(1)求 的分布列和均值;
的分布列和均值;
(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2015·新课标1卷)执行右面的程序框图,如果输入的t=0.01,则输出的n=( )

A.5
B.6
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知向量
 ,设
,设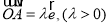 ,向量
,向量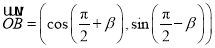 .
.(1)若
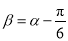 ,求向量
,求向量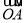 与
与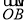 的夹角;
的夹角;(2)若
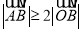 对任意实数
对任意实数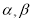 都成立,求实数
都成立,求实数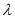 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
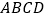 是等腰梯形,
是等腰梯形,  ,
,  ,
,  ,在梯形
,在梯形  中,
中,  ,且
,且 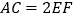 ,
,  平面
平面 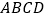 .
.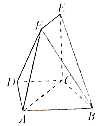
(1)求证: 平面
平面  ;
;
(2)若二面角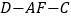 的大小为
的大小为  ,求
,求  的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为  ,其中左焦点为
,其中左焦点为  .
.
(1)求椭圆 的方程;
的方程;
(2)过 的直线
的直线  与椭圆
与椭圆  相交于
相交于  两点,若
两点,若  的面积为
的面积为  ,求以
,求以  为圆心且与直线
为圆心且与直线  相切的圆的方程.
相切的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)设函数 ,求
,求  的最大值;
的最大值;
(2)试判断方程 在
在  内存在根的个数,并说明理由.
内存在根的个数,并说明理由.
相关试题

