【题目】
(1)设函数  ,求
,求 ![]() 的最大值;
的最大值;
(2)试判断方程 ![]() 在
在 ![]() 内存在根的个数,并说明理由.
内存在根的个数,并说明理由.
参考答案:
【答案】
(1)解:当 ![]() 时,若
时,若 ![]() ,
, ![]() ,
,
若 ![]() ,由
,由 ![]() ,可知
,可知 ![]() ,故
,故 ![]() .
.
当 ![]() 时,由
时,由 ![]() ,可得:
,可得:
![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增; ![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
可知 ![]() ,且
,且 ![]() .
.
综上可得,函数 ![]() 的最大值为
的最大值为 ![]() .
.
(2)解:方程 ![]() 在
在 ![]() 内存在唯一的根.
内存在唯一的根.
理由如下:设 ![]() ,
,
当 ![]() 时,
时, ![]() ,
,
又 ![]() ,
,
所以存在 ![]() ,使得:
,使得: ![]() .
.
因为 ![]() ,
,
所以当 ![]() 时,
时, ![]() ,
,
当 ![]() 时,
时, ![]() ,
,
所以当 ![]() 时,
时, ![]() 单调递增,
单调递增,
所以方程 ![]() 在
在 ![]() 内存在唯一的根.
内存在唯一的根.
【解析】对于(1)分段函数最值的研究,要结合分段函数的导致,分别求出最值,各段最大值的最大者就是最大值,要注意分类讨论。
对于(2)判断方程的实根个数时,往往通过函数的导致,判断函数的单调性,利用函数的零点推出结果。
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值的理解,了解极值反映的是函数在某一点附近的大小情况.
在这个区间单调递减,以及对函数的极值的理解,了解极值反映的是函数在某一点附近的大小情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
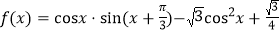
(1)求
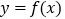 的最小正周期和递减区间;
的最小正周期和递减区间;(2)当
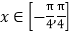 时,求
时,求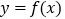 的最大值和最小值,以及取得最值时
的最大值和最小值,以及取得最值时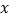 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
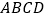 是等腰梯形,
是等腰梯形,  ,
,  ,
,  ,在梯形
,在梯形  中,
中,  ,且
,且 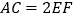 ,
,  平面
平面 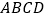 .
.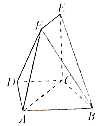
(1)求证: 平面
平面  ;
;
(2)若二面角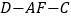 的大小为
的大小为  ,求
,求  的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为  ,其中左焦点为
,其中左焦点为  .
.
(1)求椭圆 的方程;
的方程;
(2)过 的直线
的直线  与椭圆
与椭圆  相交于
相交于  两点,若
两点,若  的面积为
的面积为  ,求以
,求以  为圆心且与直线
为圆心且与直线  相切的圆的方程.
相切的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图程序框图,如果输入的a=4,b=6,那么输出的n=( )

A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的程序框图表示的算法中,输入三个实数a,b,c,要求输出的x是这三个数中最大的数,那么在空白的判断框中,应该填入( )

A.x>c
B.c>x
C.c>b
D.c>a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的程序框图运行程序后,输出的结果是31,则判断框中的整数H=( )

A.3
B.4
C.5
D.6
相关试题

