【题目】在平面直角坐标系xOy中,已知向量![]() ,设
,设![]() ,向量
,向量![]() .
.
(1)若![]() ,求向量
,求向量![]() 与
与![]() 的夹角;
的夹角;
(2)若![]() 对任意实数
对任意实数![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)向量![]() 与
与![]() 的夹角为
的夹角为![]() ;(2)
;(2)![]() 。
。
【解析】试题分析:
(1)由题意结合平面向量的坐标表示,结合平面向量的数量积运算法则可得![]() . 则向量
. 则向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(2)原问题等价于![]() 任意实数
任意实数![]() 都成立.分离参数可得
都成立.分离参数可得![]() 任意实数
任意实数![]() 都成立.结合三角函数的性质求解关于实数
都成立.结合三角函数的性质求解关于实数![]() 的不等式可得
的不等式可得![]() .
.
试题解析:
(1)由题意, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
,
设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
所以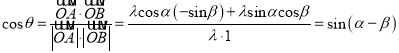 .
.
因为![]() ,即
,即![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,即向量
,即向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(2)因为![]() 对任意实数
对任意实数![]() 都成立,而
都成立,而![]() ,
,
所以![]() ,即
,即![]() 任意实数
任意实数![]() 都成立. .
都成立. .
因为![]() ,所以
,所以![]() 任意实数
任意实数![]() 都成立.
都成立.
所以![]() 任意实数
任意实数![]() 都成立.
都成立.
因为![]() ,所以
,所以![]() 任意实数
任意实数![]() 都成立.
都成立.
所以![]() ,即
,即![]() ,
,
又因为![]() ,所以
,所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①函数
 是奇函数;
是奇函数;②将函数
 的图像向左平移
的图像向左平移 个单位长度,得到函数
个单位长度,得到函数 的图像;
的图像;③若
 是第一象限角且
是第一象限角且 ,则
,则 ;
;④
 是函数
是函数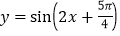 的图像的一条对称轴;
的图像的一条对称轴;⑤函数
 的图像关于点
的图像关于点 中心对称。
中心对称。其中,正确的命题序号是______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为  ,
,  ,
,  ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用  表示乙队的总得分.
表示乙队的总得分.
(1)求 的分布列和均值;
的分布列和均值;
(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2015·新课标1卷)执行右面的程序框图,如果输入的t=0.01,则输出的n=( )

A.5
B.6
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
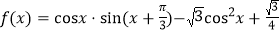
(1)求
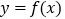 的最小正周期和递减区间;
的最小正周期和递减区间;(2)当
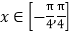 时,求
时,求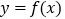 的最大值和最小值,以及取得最值时
的最大值和最小值,以及取得最值时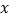 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
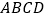 是等腰梯形,
是等腰梯形,  ,
,  ,
,  ,在梯形
,在梯形  中,
中,  ,且
,且 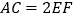 ,
,  平面
平面 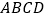 .
.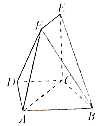
(1)求证: 平面
平面  ;
;
(2)若二面角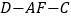 的大小为
的大小为  ,求
,求  的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为  ,其中左焦点为
,其中左焦点为  .
.
(1)求椭圆 的方程;
的方程;
(2)过 的直线
的直线  与椭圆
与椭圆  相交于
相交于  两点,若
两点,若  的面积为
的面积为  ,求以
,求以  为圆心且与直线
为圆心且与直线  相切的圆的方程.
相切的圆的方程.
相关试题

