【题目】某校高二八班选出甲、乙、丙三名同学参加级部组织的科学知识竞赛.在该次竞赛中只设成绩优秀和成绩良好两个等次,若某同学成绩优秀,则给予班级10分的班级积分,若成绩良好,则给予班级5分的班级积分.假设甲、乙、丙成绩为优秀的概率分别为 ![]() ,
, ![]() ,
, ![]() ,他们的竞赛成绩相互独立.
,他们的竞赛成绩相互独立.
(1)求在该次竞赛中甲、乙、丙三名同学中至少有一名成绩为优秀的概率;
(2)记在该次竞赛中甲、乙、丙三名同学所得的班级积分之和为随机变量ξ,求随机变量ξ的分布列和数学期望Eξ.
参考答案:
【答案】
(1)解:记“甲成绩为优秀”为事件A,“乙成绩优秀”为事件B,“丙成绩优秀”为事件C,
“甲、乙、丙至少有一名成绩为优秀”为事件E,
∵事件A、B、C是相互独立事件,事件ABC与事件E是对立事件,
∴P(E)=1﹣P( ![]() )=1﹣
)=1﹣ ![]() =
= ![]()
(2)解:ξ的所有可能取值为15,20,25,30,
P(ξ=15)=P( ![]() )=
)= ![]() =
= ![]() ,
,
P(ξ=20)=P(A ![]() )+P(
)+P( ![]() )+P(
)+P( ![]() )=
)= ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
P(ξ=30)=P(ABC)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 15 | 20 | 25 | 30 |
P |
|
|
|
|
Eξ= ![]() =
= ![]()
【解析】(1)记“甲成绩为优秀”为事件A,“乙成绩优秀”为事件B,“丙成绩优秀”为事件C,“甲、乙、丙至少有一名成绩为优秀”为事件E,由事件A、B、C是相互独立事件,事件ABC与事件E是对立事件,能求出在该次竞赛中甲、乙、丙三名同学中至少有一名成绩为优秀的概率.(2)ξ的所有可能取值为15,20,25,30,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=(|x﹣a2|+|x﹣2a2|﹣3a2),若对于任意x∈R,都有f(x﹣2)≤f(x),则实数a的取值范围是( )
A.[﹣ ,
,  ]
]
B.[﹣ ,
,  ]
]
C.[﹣ ,
,  ]
]
D.[﹣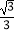 ,
, 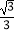 ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在以
在以 为直径的圆
为直径的圆 上,
上, 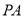 垂直与圆
垂直与圆 所在平面,
所在平面,  为
为 的垂心.
的垂心.(1)求证:平面
 平面
平面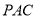 ;
;(2)若
 ,点
,点 在线段
在线段 上,且
上,且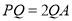 ,求三棱锥
,求三棱锥 的体积.
的体积.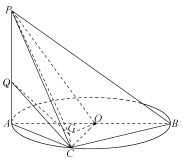
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业招聘会的现场,所有应聘者的初次面试都由张、王、李三位专家投票决定是否进入下一轮测试,张、王、李三位专家都有“通过”、“待定”、“淘汰”三类票各一张,每个应聘者面试时,张、王、李三位专家必须且只能投一张票,每人投三类票中的任意一类的概率均为
 ,且三人投票相互没有影响,若投票结果中至少有两张“通过”票,则该应聘者初次面试获得“通过”,否则该应聘者不能获得“通过”.
,且三人投票相互没有影响,若投票结果中至少有两张“通过”票,则该应聘者初次面试获得“通过”,否则该应聘者不能获得“通过”.
(1)求应聘者甲的投票结果获得“通过”的概率;
(2)记应聘者乙的投票结果所含“通过”和“待定”票的票数之和为X,求X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣lnx﹣1,g(x)=k(f(x)﹣x)+
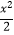 ,(k∈R).
,(k∈R).
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)求函数g(x)的单调区间;
(3)当1<k<3,x∈(1,e)时,求证:g(x)>﹣ (1+ln3).
(1+ln3). -
科目: 来源: 题型:
查看答案和解析>>【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为
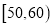 ,
, 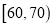 ,…,
,…, 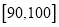 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).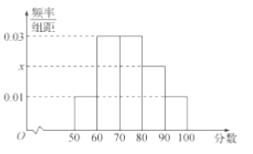
(1)求频率分布直方图中的
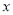 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求
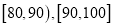 两组中至少有1人被抽到的概率.
两组中至少有1人被抽到的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
A.2,
B.4,3
C.4,
D.2,1
相关试题

