【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
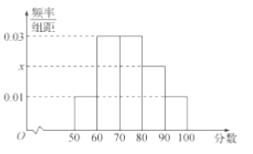
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求![]() 两组中至少有1人被抽到的概率.
两组中至少有1人被抽到的概率.
参考答案:
【答案】(1)见解析;(2)![]() .(3)
.(3)![]() .
.
【解析】试题分析:(1)由各个矩形的面积和为![]() 可得
可得![]() ,各矩形中点横坐标对应频率之积求和即可得平均数,设中位数为
,各矩形中点横坐标对应频率之积求和即可得平均数,设中位数为![]() 分,利用
分,利用![]() 左右两边面积为
左右两边面积为![]() 可得中位数;(2)根据直方图可得50名学生中成绩不低于70分的频率,即可估计这次测试成绩不低于70分的人数;(3)利用列举法,确定基本事件的个数,即利用古典概型概率公式可求出两组中至少有1人被抽到的概率的概率.
可得中位数;(2)根据直方图可得50名学生中成绩不低于70分的频率,即可估计这次测试成绩不低于70分的人数;(3)利用列举法,确定基本事件的个数,即利用古典概型概率公式可求出两组中至少有1人被抽到的概率的概率.
试题解析:(1)由频率分布直方图可得第4组的频率为![]()
![]() ,
,
故![]() .
.
故可估计所抽取的50名学生成绩的平均数为
![]()
![]()
![]() (分).
(分).
由于前两组的频率之和为![]() ,前三组的频率之和为
,前三组的频率之和为![]() ,故中位数在第3组中.
,故中位数在第3组中.
设中位数为![]() 分,
分,
则有![]() ,所以
,所以![]() ,
,
即所求的中位数为![]() 分.
分.
(2)由(1)可知,50名学生中成绩不低于70分的频率为![]() ,
,
由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为![]() .
.
(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在![]() 这组的3名学生分别为
这组的3名学生分别为![]() ,
, ![]() ,
, ![]() ,成绩在
,成绩在![]() 这组的2名学生分别为
这组的2名学生分别为![]() ,
, ![]() ,成绩在
,成绩在![]() 这组的1名学生为
这组的1名学生为![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共20种.
共20种.
其中![]() 两组中没有人被抽到的可能结果为
两组中没有人被抽到的可能结果为![]() ,只有1种,
,只有1种,
故![]() 两组中至少有1人被抽到的概率为
两组中至少有1人被抽到的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业招聘会的现场,所有应聘者的初次面试都由张、王、李三位专家投票决定是否进入下一轮测试,张、王、李三位专家都有“通过”、“待定”、“淘汰”三类票各一张,每个应聘者面试时,张、王、李三位专家必须且只能投一张票,每人投三类票中的任意一类的概率均为
 ,且三人投票相互没有影响,若投票结果中至少有两张“通过”票,则该应聘者初次面试获得“通过”,否则该应聘者不能获得“通过”.
,且三人投票相互没有影响,若投票结果中至少有两张“通过”票,则该应聘者初次面试获得“通过”,否则该应聘者不能获得“通过”.
(1)求应聘者甲的投票结果获得“通过”的概率;
(2)记应聘者乙的投票结果所含“通过”和“待定”票的票数之和为X,求X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高二八班选出甲、乙、丙三名同学参加级部组织的科学知识竞赛.在该次竞赛中只设成绩优秀和成绩良好两个等次,若某同学成绩优秀,则给予班级10分的班级积分,若成绩良好,则给予班级5分的班级积分.假设甲、乙、丙成绩为优秀的概率分别为
 ,
,  ,
,  ,他们的竞赛成绩相互独立.
,他们的竞赛成绩相互独立.
(1)求在该次竞赛中甲、乙、丙三名同学中至少有一名成绩为优秀的概率;
(2)记在该次竞赛中甲、乙、丙三名同学所得的班级积分之和为随机变量ξ,求随机变量ξ的分布列和数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣lnx﹣1,g(x)=k(f(x)﹣x)+
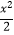 ,(k∈R).
,(k∈R).
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)求函数g(x)的单调区间;
(3)当1<k<3,x∈(1,e)时,求证:g(x)>﹣ (1+ln3).
(1+ln3). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
A.2,
B.4,3
C.4,
D.2,1 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个结论:
①若命题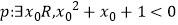 ,则p:x∈R,x2+x+1≥0;
,则p:x∈R,x2+x+1≥0;
②“(x﹣3)(x﹣4)=0”是“x﹣3=0”的充分而不必要条件;
③命题“若m>0,则方程x2+x﹣m=0有实数根”的逆否命题为:“若方程x2+x﹣m=0没有实数根,则m≤0”;
④若a>0,b>0,a+b=4,则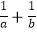 的最小值为1.
的最小值为1.
其中正确结论的个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ),数列
),数列 的前
的前 项和为
项和为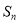 ,点
,点 在
在 图象上,且
图象上,且 的最小值为
的最小值为 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
 满足
满足 ,记数列
,记数列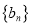 的前
的前 项和为
项和为 ,求证:
,求证:  .
.
相关试题

